Διαφορικός Λογισμός
1.Να γράψετε την εξίσωση της εφαπτομένης μιας συνάρτησης f (αν ορίζεται)σε ένα σημείο της Α(x0,f(x0)).Πότε ορίζεται η εφαπτομένη; Απάντηση Έστω f μια συνάρτηση και ένα σημείο της Α(x0,f(x0)). Αν υπάρχει το Επομένως, η εξίσωση της εφαπτομένης στο σημείο Α(x0,f(x0)) είναι y – f(x0) = λ·(x-x0).
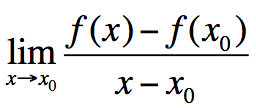και είναι ένας πραγματικός αριθμός λ, τότε ορίζουμε ως εφαπτομένη της Cf στο σημείο της Α(x0,f(x0)), την ευθεία ε που διέρχεται από το Α(x0,f(x0)) και έχει συντελεστή διεύθυνσης λ.
2.Τι ονομάζουμε παράγωγο της f στο σημείο x0 του πεδίου ορισμού της; Απάντηση
Αν μια συνάρτηση f είναι παραγωγίσιμη σε ένα σημείο x0 του πεδίου ορισμού της, το όριο 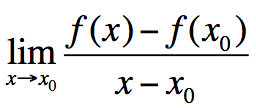ονομάζεται παράγωγος της f στο x0 και συμβολίζεται με f΄(x0). Δηλαδή: f ‘(x0) = .
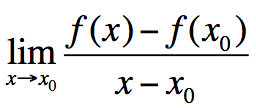3.Πότε μια συνάρτηση είναι παραγωγίσιμη σε ένα σημείο x0 του πεδίου ορισμού της; Απάντηση Μια συνάρτηση f λέμε ότι είναι παραγωγίσιμη σε ένα σημείο x0 του πεδίου ορισμού της, αν υπάρχει το ΠΑΡΑΤΗΡΗΣΗ Είναι φανερό ότι, αν το x0 είναι εσωτερικό σημείο ενός διαστήματος του πεδίου ορισμού της f, τότε η f θα είναι παραγωγίσιμη σε ένα σημείο x0 του πεδίου ορισμού της, αν και μόνο αν υπάρχουν στο ℝ τα όρια
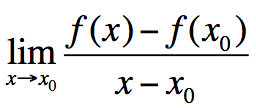και είναι πραγματικός αριθμός.
, 
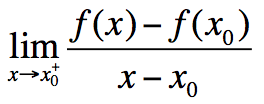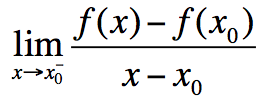(πλευρικά όρια λόγου μεταβολής) και είναι μεταξύ τους ίσα.
4.Να αποδείξετε ότι αν μια συνάρτηση f είναι παραγωγίσιμη σε ένα σημείο x0 του πεδίου ορισμού της, τότε είναι και συνεχής στο σημείο αυτό. Απάντηση Για x ≠ x0 έχουμε: ΣΧΟΛΙΟ Αν μια συνάρτηση f δεν είναι συνεχής σ’ ένα σημείο x0, τότε, σύμφωνα με το προηγούμενο θεώρημα, δεν μπορεί να είναι παραγωγίσιμη στο x0.
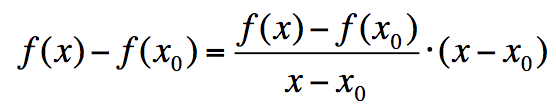,οπότε
=
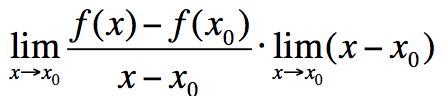= f ‘(x0)·0 = 0 ,αφού η f είναι παραγωγίσιμη στο x0. Επομένως,
= f (x0), δηλαδή η f είναι συνεχής στο x0 .
5.Πότε μια συνάρτηση f είναι παραγωγίσιμη στο πεδίο ορισμού της Α ή απλά παραγωγίσιμη; Απάντηση Έστω f μια συνάρτηση με πεδίο ορισμού ένα σύνολο Α. Θα λέμε ότι: H f είναι παραγωγίσιμη στο Α ή απλά παραγωγίσιμη, όταν είναι παραγωγίσιμη σε κάθε σημείο x0∈A .
Απάντηση Η f είναι παραγωγίσιμη σε ένα ανοικτό διάστημα (α,β) του πεδίου ορισμού της, όταν είναι παραγωγίσιμη σε κάθε σημείο x0∈(α,β).
Έστω f μια συνάρτηση με πεδίο ορισμού ένα σύνολο Α. Θα λέμε ότι:
Απάντηση Έστω f μια συνάρτηση με πεδίο ορισμού ένα σύνολο Α. Θα λέμε ότι: Η f είναι παραγωγίσιμη σε ένα κλειστό διάστημα [α,β] του πεδίου ορισμού της, όταν είναι παραγωγίσιμη σε κάθε σημείο x0∈(α,β) και επιπλέον ισχύει
.
8.Τι ονομάζουμε πρώτη παράγωγο μιας συνάρτησης f; Απάντηση Έστω f μια συνάρτηση με πεδίο ορισμού Α και Α1 τo σύνολο των σημείων του Α στα οποία αυτή είναι παραγωγίσιμη. Αντιστοιχίζοντας κάθε x∈Α1 στο f΄(x) , ορίζουμε τη συνάρτηση: f΄ : Α1 → ℝ x → f΄(x) , η οποία ονομάζεται πρώτη παράγωγος της f ή απλά παράγωγος της f. H πρώτη παράγωγος της f συμβολίζεται και με df/dx που διαβάζεται “ντε εφ προς ντε χι”. Για πρακτικούς λόγους την παράγωγο συνάρτηση y = f΄(x) θα τη συμβολίζουμε και με y = (f(x))΄.
9.Τι ονομάζουμε δεύτερη παράγωγο μιας συνάρτησης f; Απάντηση Έστω f μια συνάρτηση με πεδίο ορισμού Α και Α1 τo σύνολο των σημείων του Α στα οποία αυτή είναι παραγωγίσιμη.Αν υποθέσουμε ότι το Α1 είναι διάστημα ή ένωση διαστημάτων, τότε η παράγωγος της f΄, αν υπάρχει , λέγεται δεύτερη παράγωγος της f και συμβολίζεται με f΄΄.
10.Να δείξετε οτι η σταθερή συνάρτηση f(x) = c , c∈ℝ είναι παραγωγίσιμη στο ℝ με f΄(x) = 0 ,δηλαδή (c)΄= 0 . Απάντηση
11.Να δείξετε οτι η συνάρτηση f(x) = x είναι παραγωγίσιμη στο ℝ με f΄(x) = 1 ,δηλαδή (x)΄= 1 . Απάντηση
12.Να δείξετε οτι η συνάρτηση f(x) = xν ,ν∈ℕ -{0,1} είναι παραγωγίσιμη στο ℝ με f΄(x) = ν·xν-1 ,δηλαδή (xν)΄= ν·xν-1 . Απάντηση
13.Να δείξετε οτι η συνάρτηση Απάντηση
είναι παραγωγίσιμη στο (0,+∞) με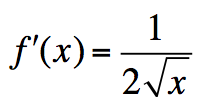 
.
14.Να γράψετε την παράγωγο της συνάρτησης f (x) = ημx. Απάντηση
Η συνάρτηση f (x) = ημx ,είναι παραγωγίσιμη στο ℝ με f΄(x) = συνx , δηλαδή (ημx)΄= συνx.
15.Να γράψετε την παράγωγο της συνάρτησης f (x) = συνx. Απάντηση Η συνάρτηση f (x) = συνx ,είναι παραγωγίσιμη στο ℝ με f΄(x) = -ημx , δηλαδή (συνx)΄= -ημx.