Ολοκληρωτικός Λογισμός
1.Τι ονομάζουμε αρχική συνάρτηση ή παράγουσα της f; Απάντηση Έστω f μια συνάρτηση ορισμένη σε ένα διάστημα Δ. Αρχική συνάρτηση ή παράγουσα της f στο Δ ονομάζεται κάθε συνάρτηση F που είναι παραγωγίσιμη στο Δ και ισχύει F΄(x) = f (x) , για κάθε x ∈ℝ .
Απάντηση Κάθε συνάρτηση της μορφής G(x) = F(x) + c, όπου c∈ℝ, είναι μια παράγουσα της f στο Δ, αφού G΄(x) = (F(x) + c)΄= F΄(x) = f(x) , για κάθε x∈Δ. Έστω G είναι μια άλλη παράγουσα της f στο Δ. Τότε για κάθε x∈Δ ισχύουν F΄(x) = f(x) και G΄(x) = f(x), οπότε G΄(x) = F΄(x), για κάθε x∈Δ. Άρα υπάρχει σταθερά c τέτοια ώστε G(x) = F(x) + c, για κάθε x∈Δ.
Απάντηση Έστω μια συνάρτηση f συνεχής στο [α,β] . Με τα σημεία α = x0 < x1 < x2 < … < xν = β χωρίζουμε το διάστημα [α,β] σε ν ισομήκη υποδιαστήματα μήκους Δx = Στη συνέχεια επιλέγουμε αυθαίρετα ένα το οποίο συμβολίζεται, σύντομα, ως εξής: Αποδεικνύεται ότι, “Το όριο του αθροίσματος Sv , δηλαδή το Το παραπάνω όριο (1) ονομάζεται ορισμένο ολοκλήρωμα της συνεχούς συνάρτησης f από το α στο β, συμβολίζεται με Δηλαδή,
.
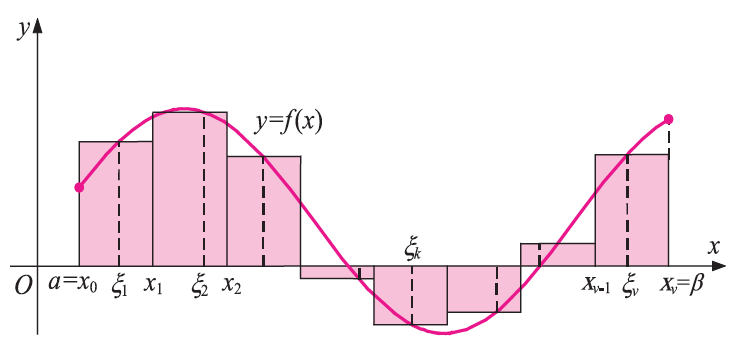
, για κάθε k∈ {1 , 2 , … ,ν}, και σχηματίζουμε το άθροισμα
,
.
(1) υπάρχει στο ℝ και είναι ανεξάρτητο από την επιλογή των ενδιάμεσων σημείων ξκ ”.
και διαβάζεται “ολοκλήρωμα της f από το α στο β”.
4.Αν c > 0, τότε ποιο εμβαδόν εκφράζει το Απάντηση Αν c > 0, τότε το ;
εκφράζει το εμβαδόν ενός ορθογωνίου παραλληλογράμμου με βάση β-α και ύψος c.
Απάντηση Αν f(x) ≥ 0 για κάθε x∈ [α , β], τότε το ολοκλήρωμα Δηλαδή ΣΧΟΛΙΟ Αν f(x) ≥ 0 , τότε ,αν f(x) ≥ 0 για κάθε x∈ [α , β] ;
δίνει το εμβαδόν E (Ω) του χωρίου Ω που περικλείεται από τη γραφική παράσταση της f ,τον άξονα x΄x και τις ευθείες x = α και x = β.
= E(Ω).
≥ 0
Απάντηση
.
Απάντηση Γνωρίζουμε ότι η συνάρτηση F(x) = G(β) = F(β) + G(α) = = G(β) – G(α). (Θ.Θ.Ο.Λ.)
είναι μια παράγουσα της f στο [α , β] . Επειδή και η G είναι μια παράγουσα της f στο [α , β], θα υπάρχει c∈ℝ τέτοιο, ώστε G(x) = F(x) + c . (1)
Από την (1), για x = α , έχουμε G(α) = F(α) + c = = c , οπότε c = G(α).
Επομένως, G(x) = F(x) + G(α), οπότε, για x = β, έχουμε : + G(α) και άρα
= G(β) – G(α) .
