Μετρικές Σχέσεις
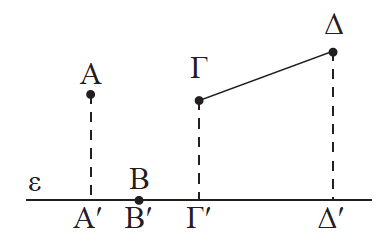
Απάντηση Έστω μία ευθεία ε και ένα σημείο Α που δεν ανήκει σε αυτή. Το ίχνος Αʹ της καθέτου που φέρουμε από το Α προς την ε το λέμε ορθή προβολή ή απλώς προβολή του Α στην ευθεία ε. Αν το σημείο είναι σημείο της ευθείας, π.χ. το Β, τότε ως προβολή του Βʹ πάνω στην ε θεωρούμε το ίδιο το Β. Τέλος ορθή προβολή του τμήματος ΓΔ πάνω στην ευθεία ε λέμε το τμήμα ΓʹΔʹ που έχει ως άκρα τις ορθές προβολές Γʹ, Δʹ των άκρων Γ, Δ, αντίστοιχα, του τμήματος ΓΔ πάνω στην ε.
Απάντηση Έστω λοιπόν ένα ορθογώνιο τρίγωνο ΑΒΓ και Δ η προβολή της κορυφής Α στην υποτείνουσα ΒΓ. Θέλουμε να αποδείξουμε ότι ΑΒ 2 = ΒΓ ∙ ΒΔ και ΑΓ 2 = ΒΓ ∙ ΓΔ. Για την πρώτη σχέση αρκεί να αποδείξουμε ότι ΣΧΟΛΙΟ Διαιρώντας τις ΑΒ 2 = ΒΓ ∙ ΒΔ και ΑΓ 2 = ΒΓ ∙ ΓΔ κατά μέλη προκύπτει το εξής πόρισμα: Σε κάθε ορθογώνιο τρίγωνο, ο λόγος των τετραγώνων των κάθετων πλευρών του είναι ίσος με το λόγο των προβολών τους πάνω στην υποτείνουσα.
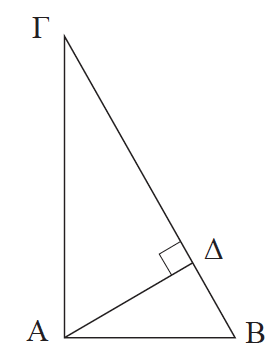
,δηλαδή ότι τα τρίγωνα ΑΒΓ και ΔΒΑ είναι όμοια, το οποίο ισχύει αφού Â = Δ̂ = 90° και η B̂ είναι κοινή. Όμοια αποδεικνύεται και η σχέση ΑΓ 2 = ΒΓ ∙ ΓΔ.
Απάντηση Θέλουμε δηλαδή να αποδείξουμε ότι AB 2 + ΑΓ 2 = ΒΓ 2 ή α 2 = β 2 + γ 2 .Σύμφωνα με το προηγούμενο θεώρημα έχουμε: ΑΒ 2 = ΒΓ ∙ ΒΔ και ΑΓ 2 = ΒΓ ∙ ΓΔ . ΑΒ 2 + ΑΓ 2 = ΒΓ ∙ ΒΔ + ΒΓ ∙ ΓΔ = ΒΓ(ΒΔ + ΓΔ) = ΒΓ ∙ ΒΓ = ΒΓ 2.

Με πρόσθεση των ισοτήτων κατά μέλη προκύπτει ότι:
Απάντηση Πάνω στις πλευρές Ox, Oy ορθής γωνίας xÔy θεωρούμε αντίστοιχα τμήματα ΟΔ = ΑΒ και ΟΕ = ΑΓ. Επειδή το τρίγωνο ΟΔΕ είναι ορθογώνιο σύμφωνα με το Πυθαγόρειο θεώρημα και την υπόθεση, έχουμε ΔΕ 2 = ΟΔ 2 + ΟΕ 2 = ΑΒ 2 +ΑΓ 2 = ΒΓ 2. Άρα ΔΕ = ΒΓ. Επομένως τα τρίγωνα ΑΒΓ και ΟΔΕ είναι ίσα, γιατί έχουν και τις τρεις πλευρές ίσες, οπότε θα είναι Â = Ô = 90°, που είναι το ζητούμενο.

Απάντηση Έστω ΑΔ το ύψος του ορθογώνιου τριγώνου ΑΒΓ , που αντιστοιχεί στην υποτείνουσα. Θα αποδείξουμε ότι ΑΔ 2 = ΒΔ ∙ ΔΓ .Τα τρίγωνα ΑΒΔ και ΓΑΔ είναι όμοια, αφού είναι ορθογώνια και Â1 = Γ̂ ως συμπληρωματικές της B̂ . Επομένως, οι πλευρές τους είναι ανάλογες, δηλαδή

, οπότε ΑΔ 2 = ΒΔ ∙ ΔΓ.
Απάντηση Αν δηλαδή σε ένα τρίγωνο ΑΒΓ είναι π.χ. Â < 90° και ΑΔ η προβολή της πλευράς γ πάνω στη β, τότε θα αποδείξουμε οτι ισχύει α 2 = β 2 + γ 2 – 2β ∙ ΑΔ . Από τα ορθογώνια τρίγωνα ΔΒΓ, ΔΒΑ έχουμε, με εφαρμογές του Πυθαγόρειου θεωρήματος αντίστοιχα: α 2 = ΔΒ 2 + ΔΓ 2 και ΔΒ 2 = γ 2 – ΑΔ 2 .Επειδή είναι Â < 90° τα Δ, Γ βρίσκονται προς το ίδιο μέρος του Α και ειδικότερα: →αν Γ̂ < 90° το Δ είναι μεταξύ των Α, Γ, οπότε ΔΓ = β – ΑΔ. →αν Γ̂ > 90° το Γ είναι μεταξύ των Α, Δ, οπότε ΔΓ = ΑΔ – β. Από τις δύο τελευταίες ισότητες προκύπτει ότι ΔΓ 2 = (β – ΑΔ) 2 = β 2 + ΑΔ 2 – 2β ∙ ΑΔ. α 2 = γ 2 – ΑΔ 2 + β 2 + ΑΔ 2 – 2β ∙ ΑΔ = β 2 + γ 2 – 2β ∙ ΑΔ, δηλαδή η ζητούμενη ισότητα. →αν τέλος Γ̂ = 90°, το Δ συμπίπτει με το Γ και το ορθογώνιο τρίγωνο ΓΑΒ δίνει α 2 = γ 2 – β 2 που γράφεται α 2 = β 2 + γ 2 – 2β∙ΑΔ , αφού ΑΔ = β.
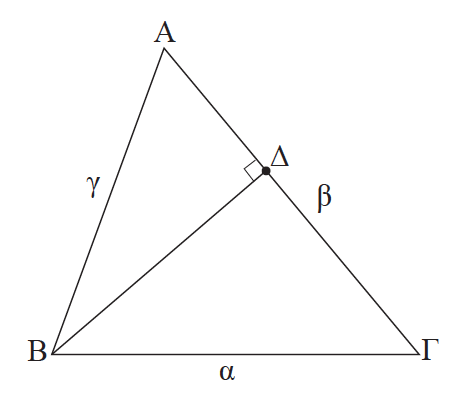

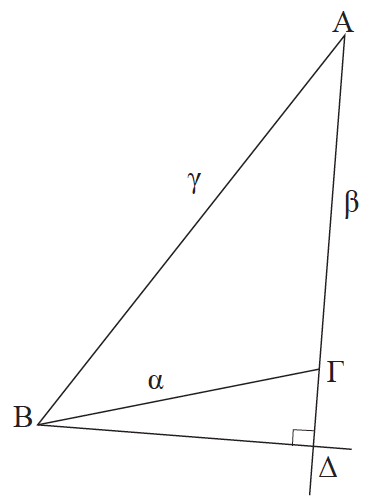
Με αντικατάσταση αυτής της σχέσης και της ΔΒ 2 = γ 2 – ΑΔ 2 στην α 2 = ΔΒ 2 + ΔΓ 2 προκύπτει ότι:
Απάντηση Αν δηλαδή σε ένα τρίγωνο ΑΒΓ είναι π.χ. Â > 90° και ΑΔ η προβολή της πλευράς γ πάνω στη β, τότε θα αποδείξουμε οτι ισχύει α 2 = β 2 + γ 2 + 2β ∙ ΑΔ . Από τα ορθογώνια τρίγωνα ΔΒΓ, ΔΒΑ έχουμε, με εφαρμογές του Πυθαγόρειου θεωρήματος αντίστοιχα: α 2 = ΔΒ 2 + ΔΓ 2 και ΔΒ 2 = γ 2 – ΑΔ 2 .Επειδή είναι Â > 90° το Δ βρίσκεται στην προέκταση της ΓΑ προς το Α και επομένως ΔΓ = β + ΑΔ οπότε ΔΓ 2 = (β + ΑΔ) 2 = β 2 + ΑΔ 2 + 2β ∙ ΑΔ. Με αντικατάσταση των σχέσεων ΔΒ 2 = γ 2 – ΑΔ 2 και ΔΓ 2 = (β + ΑΔ) 2 = β 2 + ΑΔ 2 + 2β ∙ΑΔ α 2 = γ 2 – ΑΔ 2 + β 2 + ΑΔ 2 + 2β∙ΑΔ = β 2 + γ 2 + 2β∙ΑΔ. ΣΧΟΛΙΟ Από το Πυθαγόρειο θεώρημα και τα προηγούμενα θεωρήματα προκύπτει άμεσα ότι σε κάθε τρίγωνο ΑΒΓ έχουμε:
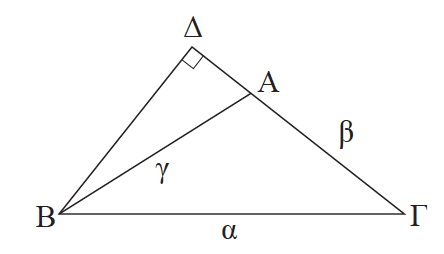
στη σχέση α 2 = ΔΒ 2 + ΔΓ 2, προκύπτει η ζητούμενη ισότητα ,
Απάντηση Σε κάθε τρίγωνο ΑΒΓ ισχύουν οι ισοδυναμίες: α 2 > β 2 + γ 2, αν και μόνο αν Â > 90° α 2 = β 2 + γ 2, αν και μόνο αν Â = 90° α 2 < β 2 + γ 2, αν και μόνο αν Â < 90° Σύμφωνα με το πόρισμα αυτό και επειδή σε κάθε τρίγωνο η μεγαλύτερη πλευρά βρίσκεται απέναντι στη μεγαλύτερη γωνία, συγκρίνοντας το τετράγωνο της μεγαλύτερης πλευράς ενός τριγώνου με το άθροισμα των τετραγώνων των άλλων πλευρών του, διαπιστώνουμε αν το τρίγωνο είναι οξυγώνιο, ορθογώνιο ή αμβλυγώνιο.
Για να βρούμε το είδος ως προς τις γωνίες ενός τριγώνου ΑΒΓ ,αν γνωρίζουμε τις πλευρές του ,βασιζόμαστε στο παρακάτω Πόρισμα:
9.Να γράψετε το νόμο των συνημιτόνων. Απάντηση Σε κάθε τρίγωνο ΑΒΓ ισχύει η σχέση: α 2 = β 2 + γ 2 – 2βγ ∙ συνÂ. β 2 = α 2 + γ 2 – 2αγ ∙ συνB̂. γ 2 = α 2 + β 2 – 2αβ ∙ συνΓ̂.
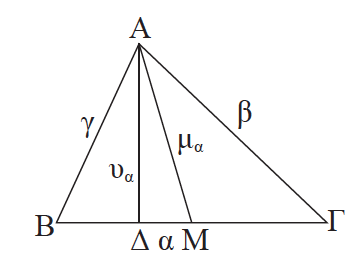
Απάντηση Έστω τρίγωνο ΑΒΓ, η διάμεσος AM = μα και το ύψος ΑΔ. Αν ΑΓ > ΑΒ, τότε το ίχνος Δ του υα βρίσκεται μεταξύ των Β, Μ και ΑM̂ Γ > 90°, ενώ ΑM̂ Β < 90°. Εφαρμόζουμε το θεώρημα αμβλείας γωνίας στο τρίγωνο ΑΜΓ και το θεώρημα οξείας γωνίας στο τρίγωνο ΑΜΒ. Τότε θα έχουμε ότι: i. ΑΓ 2 = ΑΜ 2 + ΜΓ 2 + 2ΜΓ∙ΜΔ και ii. ΑΒ 2 = ΑΜ 2 + ΜΒ 2 – 2ΜΒ∙ΜΔ Προσθέτοντας κατά μέλη αυτές τις σχέσεις και λαμβάνοντας υπόψη ότι ΜΒ = ΜΓ έχουμε: ΑΓ 2 + ΑΒ 2 = 2ΑΜ 2 + 2ΜΒ 2 = 2ΑΜ 2 + Ανάλογα έχουμε και τους ακόλουθους τύπους: ΣΧΟΛΙΟ Από τους τύπους αυτούς μπορούμε να υπολογίσουμε τα τετράγωνα των διαμέσων ως συνάρτηση των πλευρών του τριγώνου:
=
ή
.
και
.
Απάντηση Έστω ότι ΑΓ > ΑΒ. Αφαιρώντας κατά μέλη τις σχέσεις i. ΑΓ 2 = ΑΜ 2 + ΜΓ 2 + 2ΜΓ∙ΜΔ και ii. ΑΒ 2 = ΑΜ 2 + ΜΒ 2 – 2ΜΒ∙ΜΔ (1ο θεώρημα διαμέσων) ,βρίσκουμε ότι ΑΓ 2 – ΑΒ 2 = 4ΜΒ ∙ ΜΔ =

ή β 2 – γ 2 = 2α ∙ ΜΔ.
12.Nα αποδείξετε οτι αν δύο χορδές ΑΒ, ΓΔ ή οι προεκτάσεις τους τέμνονται σε ένα σημείο Ρ, τότε ισχύει ΡΑ ∙ ΡΒ = ΡΓ ∙ ΡΔ. Απάντηση Τα τρίγωνα ΡΑΓ και ΡΒΔ είναι όμοια, αφού ΡÂΓ = ΡΔ̂ Β γιατί το τετράπλευρο ΑΒΓΔ είναι εγγράψιμο και η ΡÂΓ είναι εξωτερική του γωνία και ΡΓ̂ Α = ΡB̂ Δ . Τα τρίγωνα ΡΑΓ και ΡΒΔ είναι όμοια, αφού ΡÂΓ = ΡΔ̂ Β και ΡΓ̂ Α = ΡB̂ Δ ως εγγεγραμμένες γωνίες που βαίνουν στο ίδιο τόξο . Επομένως, ισχύει ότι
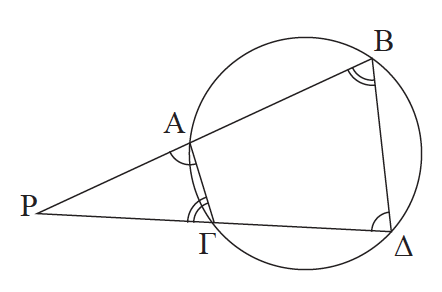
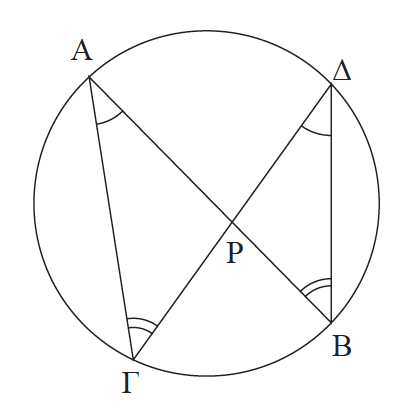
ή ΡΑ ∙ ΡΒ = ΡΓ ∙ ΡΔ .
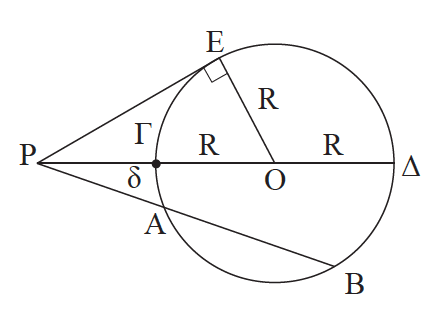
Απάντηση Φέρουμε την ευθεία ΡΟ η οποία τέμνει τον κύκλο στα σημεία Γ και Δ. Θέτουμε ΟΡ = δ, οπότε από το προηγουμενο θεώρημα έχουμε ότι: ΡΑ ∙ ΡΒ = ΡΓ ∙ ΡΔ = (δ – R)(δ + R)= δ 2 – R 2 . Από το Πυθαγόρειο θεώρημα στο τρίγωνο ΡΟΕ προκύπτει ότι PE 2 = PO 2 – OE 2= δ 2 – R 2 . Άρα ΡΕ2 = ΡΑ ∙ ΡΒ. ΣΧΟΛΙΟ Στην προηγούμενη απόδειξη είδαμε ότι αν μια ευθεία διέρχεται από ένα εξωτερικό σημείο Ρ κύκλου (Ο, R) και τέμνει τον κύκλο σε σημεία Α, Β τότε ΡΑ ∙ ΡΒ = δ 2 – R 2. Όμοια αποδεικνύεται ότι ΡΑ ∙ ΡΒ = R 2 – δ 2, αν το Ρ είναι εσωτερικό σημείο του κύκλου.
14.Τι ονομάζουμε δύναμη ενός σημείου ως προς κύκλο; Απάντηση Έστω σημείο Ρ και κύκλος (Ο, R) ,με ΟΡ = δ .Η διαφορά δ 2 – R 2 λέγεται δύναμη του σημείου Ρ ως προς τον κύκλο (O, R) και συμβολίζεται ΣΧΟΛΙΟ Από τον ορισμό της δύναμης σημείου ως προς κύκλο καταλαβαίνουμε ότι ουσιαστικά εκφράζει τη σχετική θέση του σημείου Ρ ως προς τον κύκλο (O, R), καθώς εξαρτάται μόνο από το δ, δηλαδή την απόσταση του Ρ από το κέντρο του κύκλου. Επομένως, έχουμε ότι: →Το Ρ είναι εξωτερικό σημείο του κύκλου (O, R) αν και μόνο αν →Το Ρ είναι εσωτερικό σημείο του κύκλου (O, R) αν και μόνο αν →Το Ρ είναι σημείο του κύκλου (O, R) αν και μόνο αν
= δ 2 – R 2 = ΟΡ 2 – R 2.
.
.
.
