Σχολικό βιβλίο – Κεφάλαιο 6 ¨ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΤΩΝ ΣΥΝΑΡΤΗΣΕΩΝ¨ (εμπλουτισμένο)
Καρτεσιανές συντεταγμένες
Ορθοκανονικό σύστημα συντεταγμένων ονομάζεται το καρτεσιανό σύστημα συντεταγμένων που έχει τους άξονες του κάθετους.
Άξονας τετμημένων ή άξονας των x, ονομάζεται ο οριζόντιος άξονας x΄x.
Άξονας τεταγμένων ή άξονας των y, ονομάζεται ο κατακόρυφος άξονας y΄y .
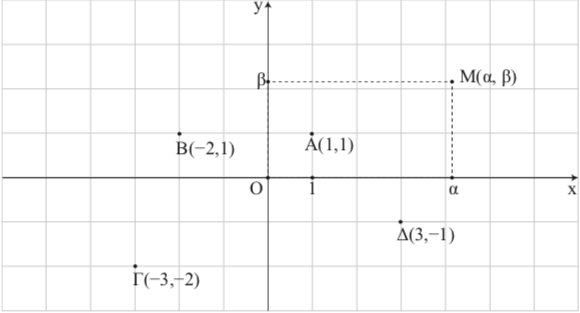
Καρτεσιανό επίπεδο ονομάζουμε ένα επίπεδο στο οποίο ορίζουμε ένα σύστημα συντεταγμένων.
Καρτεσιανό σύστημα συντεταγμένων ονομάζεται ένα ζεύγος δύο αξόνων, οι οποίοι έχουν κοινή αρχή Ο και είναι αριθμημένοι με τις ίδιες μονάδες μήκους.
⇒Κάθε διατεταγμένο ζεύγος αριθμών (α , β) σε ένα καρτεσιανό σύστημα συντεταγμένων παριστάνεται από ένα σημείο Μ και αντιστρόφως.
⇒Τετμημένη ενός σημείου Μ(α , β) ονομάζεται ο αριθμός α που αναφέρεται πρώτος στο διατεταγμένο ζεύγος .
⇒Τεταγμένη ενός σημείου Μ(α , β) ονομάζεται ο αριθμός β που αναφέρεται δεύτερος στο διατεταγμένο ζεύγος .
⇒Οι κάθετοι άξονες x΄x (άξονας τετμημένων) και y΄y (άξονας τεταγμένων) χωρίζουν το επίπεδο σε 4 μέρη που ονομάζονται τεταρτημόρια.
ΠΡΟΣΟΧΗ
- Τα σημεία του άξονα x΄x έχουν τεταγμένη 0, ενώ τα σημεία του άξονα y΄y έχουν τετμημένη 0 .
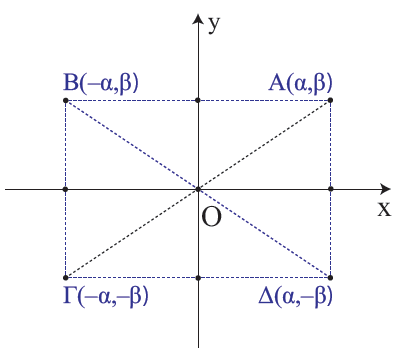
- Tο συμμετρικό του A(α , β) ως προς τον άξονα x′x είναι το σημείο Δ(α , ‒β), που έχει ίδια τετμημένη και αντίθετη τεταγμένη .
- Το συμμετρικό του A(α , β) ως προς τον άξονα y′y είναι το σημείο Β(‒α , β), που έχει ίδια τεταγμένη και αντίθετη τετμημένη .
- Το συμμετρικό του A(α , β) ως προς την αρχή των αξόνων είναι το σημείο Γ(‒α , ‒β), που έχει αντίθετες συντεταγμένες .
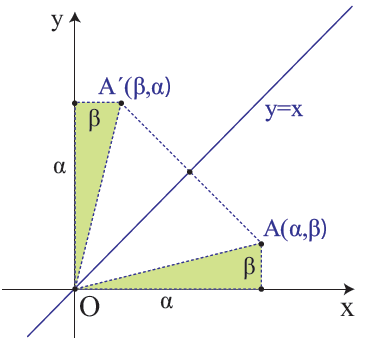
- Το συμμετρικό του A(α , β) ως προς τη διχοτόμο της 1ης και 3ης γωνίας των αξόνων ,είναι το σημείο Α′(β , α) που έχει τετμημένη την τεταγμένη του Α και τεταγμένη την τετμημένη του Α .
ΑΠΟΣΤΑΣΗ ΣΗΜΕΙΩΝ
Έστω Oxy ένα σύστημα συντεταγμένων στο επίπεδο και Α(x1,y1) και B(x2,y2) δύο σημεία αυτού. Η απόστασή τους δίνεται από τον τύπο .

Γραφική παράσταση συνάρτησης
Γραφική παράσταση Cf συνάρτησης f ονομάζεται το σύνολο όλων των σημείων του επιπέδου με συντεταγμένες της μορφής (x ,f(x)).
Λέμε επίσης ότι η εξίσωση y = f(x) ,αποτελεί την εξίσωση της καμπύλης Cf αφού οι συντεταγμένες των σημείων της Cf και μόνο αυτές επαληθεύουν την εξίσωση.
ΠΡΟΣΟΧΗ
⇒Η προβολή της γραφικής παράστασης της f στον x΄x ‘‘δείχνει’’ το πεδίο ορισμού της συνάρτησης.
⇒Η προβολή της γραφικής παράστασης της f στον y΄y ‘‘δείχνει’’ το σύνολο τιμών f(A) της συνάρτησης.
⇒Κάθε κατακόρυφη ευθεία (κάθετη στον άξονα x΄x) τέμνει τη γραφική παράσταση μιας συνάρτησης το πολύ σε ένα σημείο. (vertical line test)
(πχ ο κύκλος δεν ειναι συνάρτηση…)
Σημεία τομής γραφικής παράσταση συνάρτησης με άξονες
⇒Για να βρούμε τα κοινά σημεία της γραφικής παράστασης μιας συνάρτησης f με τον άξονα x΄x (αν υπάρχουν) πρέπει να λύσουμε την εξίσωση f(x) = 0 . Οι λύσεις της εξίσωσης θα εκφράζουν τις τετμημένες x0 των σημείων αυτών ,τα οποία θα είναι της μορφής Μ(x0 ,0).
Μια γραφική παράσταση μιας συνάρτησης f μπορεί να τέμνει τον άξονα x΄x σε απείρα σημεία!!!
⇒Για να βρούμε το σημείο που η γραφική παράσταση μιας συνάρτησης f τέμνει τον y΄y άξονα ,θέτουμε στον τύπο της όπου x το 0 , βρίσκοντας δηλαδή το f(0). Το ζητούμενο σημείο θα είναι της μορφής Μ(0 , f(0)).
Μια γραφική παράσταση μιας συνάρτησης f μπορεί να τέμνει τον άξονα y΄y το πολύ σε ένα σημείο ,αρκεί το πεδίο ορισμού της συνάρτησης να περιέχει το μηδέν.
Σχετική θέση γραφικής παράστασης συνάρτησης f ως προς τον άξονα x’x
Oι λύσεις της ανίσωσης f(x) > 0 μας δίνουν τις τετμημένες των σημείων της Cf που βρίσκονται πάνω από τον άξονα x’x.
Οι λύσεις της ανίσωσης f(x) < 0, αντιστοίχως, μας δίνουν τις τετμημένες των σημείων της Cf που είναι κάτω από τον x’x.
Οι λύσεις της εξίσωσης f(x) = 0, θα εκφράζουν τις τετμημένες των σημείων τομής Cf και άξονα x’x.
Σχετική θέση γραφικών παραστάσεων Cf, Cg
Οι λύσεις της ανίσωσης f(x) > g(x) μας δίνουν τις τετμημένες των σημείων της Cf που βρίσκονται πάνω από την Cg .
Οι λύσεις της ανίσωσης f(x) < g(x) μας δίνουν τις τετμημένες των σημείων της Cf που βρίσκονται κάτω από την Cg .
Οι λύσεις της εξίσωσης f(x) = g(x) μας δίνουν τις τετμημένες των σημείων τομής της Cf με την Cg .
Γραφικές παραστάσεις Cf , C-f
Όταν δίνεται η γραφική παράσταση μιας συνάρτησης ƒ μπορούμε, επίσης, να σχεδιάσουμε και τη γραφική παράσταση της συνάρτησης ‒ƒ, παίρνοντας τη συμμετρική της γραφικής παράστασης της ƒ ως προς τον άξονα x′x και αυτό συμβαίνει διότι η γραφική παράσταση της ‒ƒ αποτελείται από τα σημεία M′(x, ‒ƒ(x)) που είναι συμμετρικά των σημείων M(x, ƒ(x)) της γραφικής παράστασης της ƒ ως προς τον άξονα x′x.
Cf , C-f
Γραφικές παραστάσεις Cf , C|f|
Η γραφική παράστασης της συνάρτησης |f| αποτελείται από τα τμήματα της γραφικής παράστασης της f που βρίσκονται πάνω από από τον άξονα x΄x και από τα συμμετρικά, ως προς τον άξονα x΄x ,των τμημάτων της γραφικής παράστασης της f που βρίσκονται κάτω από τον άξονα αυτόν .
Cf , C|f|
Ασκησιολόγιο για την παράγραφο ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ ΣΥΝΑΡΤΗΣΗΣ θα βρείτε στη σελίδα 2
