Συστήματα
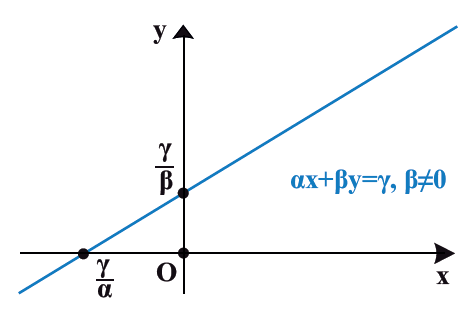
Απάντηση Η εξίσωση αx + βy = γ, με α ≠ 0 ή β ≠ 0, λέγεται γραμμική εξίσωση,καθώς παριστάνει ευθεία γραμμή.
Απάντηση Αν β ≠ 0, τότε η εξίσωση γράφεται: Επομένως η εξίσωση αυτή παριστάνει ευθεία που έχει συντελεστή διεύθυνσης Ειδικότερα: Αν α ≠ 0, τότε η ευθεία τέμνει και τους δύο άξονες , ενώ αν α = 0 , τότε η εξίσωση παίρνει τη μορφή Αν β = 0 (οπότε α ≠ 0), τότε η εξίσωση γράφεται ΣΧΟΛΙΟ Κάθε ζεύγος αριθμών που επαληθεύει μία γραμμική εξίσωση λέγεται λύση της γραμμικής εξίσωσης.
.
και τέμνει τον άξονα y’y στο σημείο
.
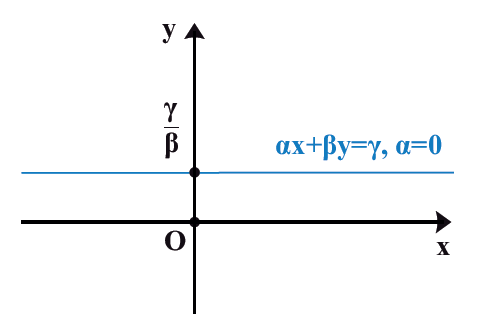
και επομένως παριστάνει ευθεία που είναι παράλληλη στον άξονα x’x και τέμνει τον άξονα y’y στο σημείο
.
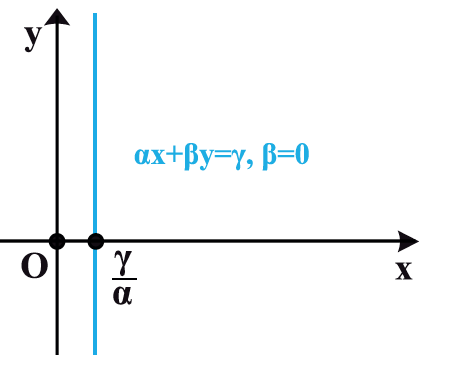
.Επομένως η εξίσωση αυτή παριστάνει ευθεία που είναι παράλληλη στον άξονα y’y και τέμνει τον άξονα x’x στο σημείο
.
Απάντηση Όταν έχουμε δύο γραμμικές εξισώσεις αx + βy = γ και α΄x + β΄y = γ΄ και ζητάμε τις κοινές λύσεις αυτών, τότε λέμε ότι έχουμε να λύσουμε ένα γραμμικό σύστημα δύο εξισώσεων με δύο αγνώστους ή, πιο σύντομα, ένα γραμμικό σύστημα 2 x 2 και γράφουμε: ΣΧΟΛΙΑ Κάθε ζεύγος αριθμών που επαληθεύει και τις δύο εξισώσεις του συστήματος λέγεται λύση του συστήματος.
Η επίλυση ενός γραμμικού συστήματος γίνεται με κατάλληλη μετατροπή του σε άλλο γραμμικό σύστημα το οποίο έχει ακριβώς τις ίδιες λύσεις με το αρχικό. Τα δύο αυτά συστήματα λέγονται ισοδύναμα συστήματα.
Απάντηση Η εξίσωση λ·(ε) και λ΄·(ε’) ,λέγεται γραμμικός συνδυασμός των εξισώσεων (ε) και (ε’).
Απάντηση Οι δύο μέθοδοι επίλυσης ενός συστήματος που γνωρίζουμε είναι η μέθοδος της αντικατάστασης και η μέθοδος των αντιθέτων συντελεστών (ή μέθοδος της απαλοιφής). Μέθοδος της αντικατάστασης. Έστω το σύστημα: Λύνουμε τη μία από τις δύο εξισώσεις ως προς έναν άγνωστο, π.χ. την πρώτη ως προς x. Έτσι το σύστημα είναι ισοδύναμο με το Αντικαθιστούμε στη δεύτερη εξίσωση το x με την παράσταση που βρήκαμε κάι έχουμε οτι Λύνουμε την εξίσωση που προκύπτει δηλαδη την Αν έχει μοναδική λύση Αν η εξίσωση ΣΧΟΛΙΟ Επειδή κάνουμε πολλά βήματα μέχρι να λύσουμε ένα σύστημα, είναι πολύ πιθανό να κάνουμε λάθος στους αριθμητικούς υπολογισμούς. Για το λόγο αυτό είναι σκόπιμο να αντικαθιστούμε τις τιμές των αγνώστων που βρήκαμε στις αρχικές εξισώσεις του συστήματος και να ελέγχουμε αν τις επαληθεύουν, δηλαδή να κάνουμε επαλήθευση του συστήματος. Μέθοδος των αντίθετων συντελεστών (ή της απαλοιφής). Έστω το σύστημα: Πολλαπλασιάζουμε τα μέλη των δύο εξισώσεων με κατάλληλους αριθμούς, ώστε οι συντελεστές του ενός αγνώστου στις εξισώσεις που θα προκύψουν να είναι αντίθετοι. Προσθέτουμε κατά μέλη τις εξισώσεις που βρήκαμε, οπότε προκύπτει εξίσωση με έναν άγνωστο, την οποία και επιλύουμε.
.
.
.
κάθώς είναι μια εξίσωση πρώτου βαθμού ως προς y .
το σύστημα είναι ισοδύναμο με το παρακάτω:
οπότε αντικάθιστούμε την τιμή
στην πρώτη εξίσωση , τη λύνουμε ως προς x και παίρνουμε για λύση
,δηλαδή το σύστημα έχει μοναδική λύση την
.
είναι αδύνατη τότε και το σύστημα είναι αδύνατο ενώ άν είναι ταυτότητα συμπεραίνουμε ότι το σύστημα έχει άπειρο πλήθος λύσεων.
.
.
Απάντηση Μπορούμε να επιλύσουμε γραφικά ένα γραμμικό σύστημα Οι δύο εξισώσεις ενός γραμμικού συστήματος 2 x 2 παριστάνουν δύο ευθείες οι οποίες μπορεί να τέμνονται οπότε και το σημείο τομής τους είναι και η λύση του συστήματος ή να είναι παράλληλες οπότε το σύστημα είναι αδύνατο ή ακόμα και να συμπίπτουν οπότε το σύστημα θα έχει άπειρο πλήθος λύσεων. Γενικά, από την επίλυση ενός γραμμικού συστήματος 2 x 2 αναμένουμε μια μόνο από τις περιπτώσεις: ΣΧΟΛΙΟ Η γραφική επίλυση ενός γραμμικού συστήματος 2 x 2 δίνει λύσεις που μπορεί να είναι προσεγγιστικές. Παρά την αδυναμία αυτή, η γραφική επίλυση ενός γραμμικού συστήματος 2 x 2 διευκολύνει πάρα πολύ σε περιπτώσεις, όπου μας ενδιαφέρουν μόνο προσεγγιστικές λύσεις του συστήματος ή, ακόμη, όταν η αλγεβρική του επίλυση είναι δυσχερής.
με το να σχεδιάσουμε τις δύο ευθείες που παριστάνουν οι εξισώσεις του και να βρούμε, εφόσον υπάρχει, το σημείο τομής τους.
Απάντηση Έστω το γραμμικό σύστημα Αρχικά θα εξετάσουμε την περίπτωση που είναι β ≠ 0 και β´≠ 0. Τότε το σύστημα γράφεται: Άν Η τεταγμένη του σημείου τομής είναι: Επομένως Στα ίδια συμπεράσματα καταλήγουμε και στην περίπτωση που είναι β=0 ή β’ =0. Συνοψίζοντας τα παραπάνω συμπεράσματα για το γραμμικό σύστημα Αν αβ΄– α΄β ≠ 0 το σύστημα έχει μοναδική λύση την Αν αβ΄– α΄β = 0 το σύστημα έχει άπειρες λύσεις ή είναι αδύνατο. .
.
,και οι εξισώσεις του παριστάνουν ευθείες ε1 και ε2 με αντίστοιχους συντελεστές
και
.
, δηλαδή αν αβ΄- α΄β ≠ 0 , τότε οι ευθείες ε1 και ε2 έχουν διαφορετικούς συντελεστές διεύθυνσης, οπότε τέμνονται σε ένα σημείο του οποίου η τετμημένη προσδιορίζεται από τη λύση της εξίσωσης:
.
. Άρα, στην περίπτωση αυτή, το σύστημα έχει μοναδική λύση την:
.
Αν , δηλαδή αν αβ΄– α΄β = 0 , τότε οι ευθείες ε1 και ε2 έχουν τον ίδιο συντελεστή διεύθυνσης, οπότε ή είναι παράλληλες ή ταυτίζονται. Αυτό σημαίνει ότι το σύστημα ή είναι αδύνατο ή έχει άπειρες λύσεις αντιστοίχως.
έχουμε:
.
Απάντηση Έστω το γραμμικό σύστημα Η παράσταση αβ΄– α΄β , συμβολίζεται με Την ορίζουσα που προκύπτει από την D, αν στη θέση των συντελεστών του x θέσουμε τους σταθερούς όρους, συμβολίζουμε με Ομοίως, την ορίζουσα που προκύπτει από την D, αν στη θέση των συντελεστών του y θέσουμε τους σταθερούς όρους, συμβολίζουμε με και ποιες Dx και Dy;
.
και λέγεται oρίζoυσα τoυ συστήματoς.
.
.
Απάντηση Το γραμμικό σύστημα Αν D ≠ 0, έχει μοναδική λύση, τη (x,y) με Αν D = 0, είναι αδύνατο ή έχει άπειρο πλήθος λύσεων.
:
και
.
Απάντηση Μία εξίσωση της μορφής αx + βy + γz = 0 , με έναν τουλάχιστον από τους συντελεστές α, β, γ διάφορο του μηδενός, λέγεται γραμμική εξίσωση με τρεις αγνώστους. ΣΧΟΛΙΟ Λύση μιας γραμμικής εξίσωσης με τρεις αγνώστους λέγεται κάθε τριάδα αριθμών που την επαληθεύει.
Απάντηση Όταν έχουμε τρεις γραμμικές εξισώσεις με τρεις αγνώστους: α1x + β1y + γ1z = δ1 , α2x + β2y + γ2z = δ2 , α3x + β3y + γ3z = δ3 και ζητάμε τις κοινές λύσεις τους, τότε λέμε ότι έχουμε να λύσουμε ένα γραμμικό σύστημα τριών εξισώσεων με τρεις αγνώστους ή, πιο σύντομα, ένα γραμμικό σύστημα 3 x 3 και γράφουμε:
12.Με ποιόν τρόπο επιλύουμε ένα γραμμικό σύστημα 3×3; Απάντηση Για την επίλυση ενός γραμμικού συστήματος 3×3 χρησιμοποιούμε μεθόδους ανάλογες με τις μεθόδους που χρησιμοποιήσαμε για την επίλυση ενός γραμμικού συστήματος 2 x 2 . Θα χρησιμοποιήσουμε τη μέθοδο της αντικατάστασης. Λύνουμε τη μία από τις τρεις εξισώσεις ως προς έναν άγνωστο και αντικαθιστούμε την εξίσωση αυτή , στις άλλες δύο εξισώσεις του συστήματος. Έτσι προκύπτει ένα γραμμικό σύστημα 2×2 που το λύνουμε με όποια απο τις τρείς μεθόδους αναφέραμε προηγουμένως. Το ζέυγος λύσεων που προκείπτει απο το γραμμικό σύστημα 2×2 το αντικαθιστούμε στην αρχική εξίσωση και έτσι υπολογίζουμε την τιμή του τρίτου αγνώστου του αρχικού μας συστήματος. Αν το γραμμικό σύστημα 2×2 είναι αδύνατο τότε και το αρχικό μας συστήμα θα είναι επίσης αδύνατο ενώ αν το γραμμικό σύστημα 2×2 έχει άπειρες λύσεις τότε και το αρχικό μας συστήμα θα έχει επίσης άπειρες λύσεις. ΣΧΟΛΙΟ Επειδή η επίλυση ενός γραμμικού συστήματος 3 x 3, όπως είδαμε παραπάνω, ανάγεται στην επίλυση ενός γραμμικού συστήματος 2 x 2, προκύπτει ότι και ένα γραμμικό σύστημα 3 x 3 ή έχει μοναδική λύση ή είναι αδύνατο ή έχει άπειρο πλήθος λύσεων.
Απάντηση Ένα σύστημα λέγεται μη γραμμικό αν μια τουλάχιστον απο τις εξισώσεις του δεν είναι γραμμική εξίσωσή. ΣΧΟΛΙΑ Ένα μή γραμμικό σύστημα μπορεί να έχει περισσότερες απο μια λύσεις. Η εξίσωση Η εξίσωση Η εξίσωση Η εξίσωση
παριστάνει κύκλο με κέντρο Ο(0,0) και ακτίνα ρ.
παριστάνει παραβολή με κορυφή το Ο(0,0) και άξονα συμμετρίας y΄y.
παριστάνει παραβολή με κορυφή το Ο(0,0) και άξονα συμμετρίας x΄x.
παριστάνει υπερβολή.
