Θεωρία στην Άλγεβρα Γενικής Παιδείας Β΄Λυκείου

Δημήτρης Ζαρκαδούλας 15/07/2016 No comments

Τριγωνομετρία

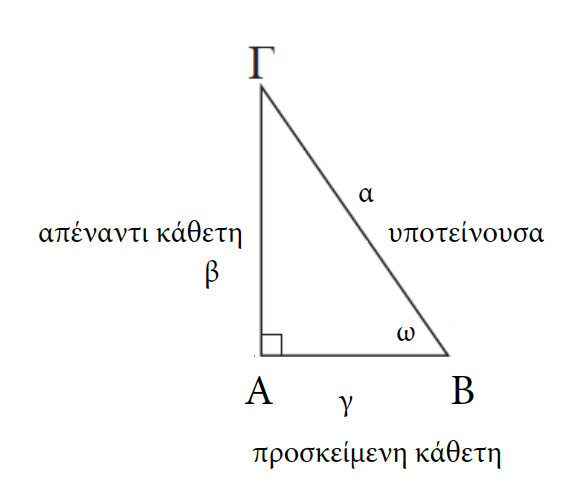
1.Πως ορίζονται οι τριγωνομετρικοί αριθμοί μιας οξείας γωνίας ω, ενός ορθογωνίου τριγώνου;

Απάντηση

Ημίτονο της γωνίας ω ορίζουμε τον σταθερό λόγο του μήκους της απέναντι κάθετης πλευράς προς το μήκος της υποτείνουσας και συμβολίζεται με ημω,

επομένως $\displaystyle \large \eta \mu \omega =\frac{\beta }{\alpha }$ .

Συνημίτονο της γωνίας ω ορίζουμε τον σταθερό λόγο του μήκους της προσκείμενης κάθετης πλευράς προς το μήκος της υποτείνουσας και συμβολίζεται με συνω,

επομένως $\displaystyle \large \sigma \upsilon \nu \omega =\frac{\gamma }{\alpha }$ .

Εφαπτομένη της γωνίας ω ορίζουμε τον σταθερό λόγο του μήκους της απέναντι κάθετης πλευράς προς το μήκος της προσκείμενης κάθετης πλευράς και συμβολίζεται με εφω,

επομένως $\displaystyle \large \varepsilon \phi \omega =\frac{\beta }{\gamma }$ .

Συνεφαπτομένη της γωνίας ω ορίζουμε τον σταθερό λόγο του μήκους της προσκείμενης κάθετης πλευράς προς το μήκος της απέναντι κάθετης πλευράς και συμβολίζεται με σφω,

επομένως $\displaystyle \large \sigma \phi \omega =\frac{ \gamma }{\beta}$ .

Απάντηση

Κλείσιμο απάντησης

2.Πως ορίζονται οι τριγωνομετρικοί αριθμοί γωνίας ω, με 0° ≤ ω ≤ 360° ;

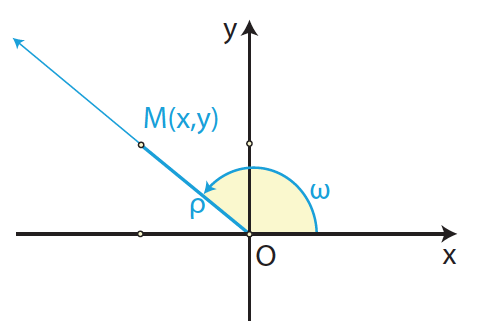
Απάντηση

Έστω Μ οποιοδήποτε σημείο του επιπέδου (διαφορετικού του Ο) με συντεταγμένες (x, y).Η γωνία xOM = ω μπορεί να πάρει τιμές από 0° έως 360° και οι τριγωνομετρικοί αριθμοί της γωνίας ω θα είναι ορίζονται ως εξής:
$\large \eta \mu \omega =\frac{y }{\rho }$ ,

$\large \sigma \upsilon \nu \omega =\frac{x }{\rho }$ ,

$\large \varepsilon \phi \omega =\frac{y }{x },x\neq 0$ ,

$\large \sigma \phi \omega =\frac{x }{y },y\neq 0$ ,

όπου .

ΣΧΟΛΙΟ

Οι παραπάνω τύποι ισχύουν για κάθε γωνία ω, θετική ή αρνητική (ο ημιάξονας Ox, στρέφεται γύρω από το Ο κατά την αρνητική φορά) ,αλλά και για κάθε γωνία που είναι μεγαλύτερη από 360^o.

Απάντηση

Κλείσιμο απάντησης

3.Πως υπολογίζουμε τους τριγωνομετρικούς αριθμούς γωνιών που είναι μεγαλύτερες απο 360^ο;

Απάντηση

Για να υπολογίσουμε τους τριγωνομετρικούς αριθμούς μιας γωνίας θ μεγαλύτερης από 360 μοίρες , διαιρούμε τη γωνία με το 360^ο ,και γράφουμε την ταυτότητα της διαίρεσης Δ = δ·π + υ ,σε μορφή θ = κ⋅360 + ω ,όπου κ είναι το πηλίκο και ω το υπόλοιπο της διαίρεσης.

Ο αριθμός κ∈ℤ δειχνει στην ουσία πόσες πλήρεις περιστροφές έχω.

Για κάθε κ∈ℤ θα ισχύει:

$\displaystyle \large \eta \mu (\kappa \cdot 360^o+\omega )=\eta \mu \omega$ ,

$\displaystyle \large \sigma \upsilon \nu (\kappa \cdot 360^o+\omega )=\sigma \upsilon \nu \omega$ ,

$\displaystyle \large \varepsilon \varphi (\kappa \cdot 360^o+\omega )=\varepsilon \phi \omega$ ,

$\displaystyle \large \sigma \varphi (\kappa \cdot 360^o+\omega )=\sigma \phi \omega$ .

Απάντηση

Κλείσιμο απάντησης

4.Τι ονομάζουμε τριγωνομετρικό κύκλο;

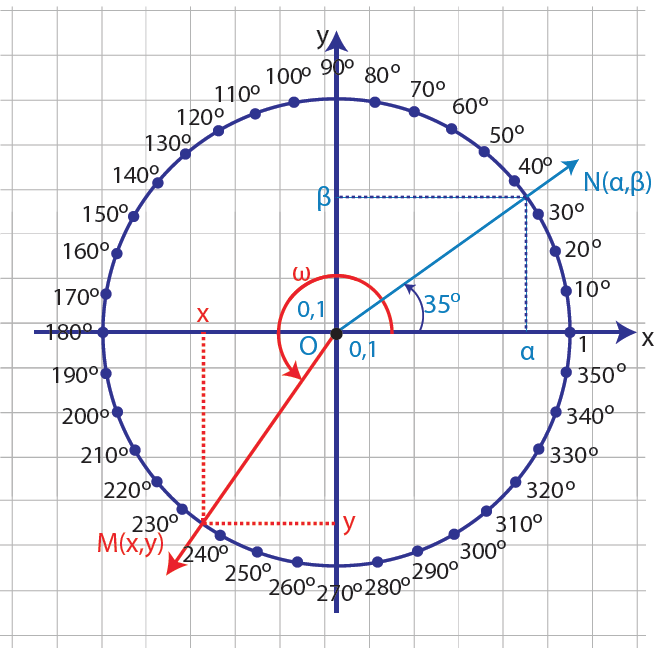
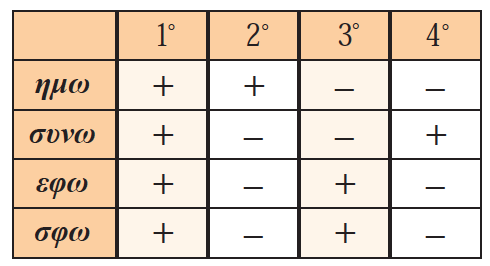
Απάντηση

Με κέντρο την αρχή Ο(0,0) ενός συστήματος συντεταγμένων και ακτίνα ρ = 1 γράφουμε έναν κύκλο. Ο κύκλος αυτός λέγεται τριγωνομετρικός κύκλος.

ΣΧΟΛΙΑ

Γενικότερα, αν η τελική πλευρά μιας γωνίας ω τέμνει τον τριγωνομετρικό κύκλο στο σημείο Μ(x, y), τότε ισχύει:

συνω = x = τετμημένη του σημείου Μ

ημω = y = τεταγμένη του σημείου Μ

→Για το λόγο αυτό ο άξονας x’x λέγεται και άξονας των συνημιτόνων, ενώ ο άξονας y’y λέγεται και άξονας των ημιτόνων.

→Η ευθεία που εφάπτεται στον κύκλο στο σημείο τομής του με τον ημιάξονα Οx (x = 1)ονομάζεται άξονας των εφαπτομένων.

→Η ευθεία που εφάπτεται στον κύκλο στο σημείο τομής του με τον ημιάξονα Oy (y = 1) ονομάζεται άξονας των συνεφαπτομένων.

→Οι τιμές του συνω και του ημω μιας γωνίας ω δεν μπορούν να υπερβούν κατ’ απόλυτη τιμή την ακτίνα του τριγωνομετρικού κύκλου, που είναι ίση με 1. Δηλαδή ισχύει:

-1 ≤ ημω ≤ 1 και -1 ≤ συνω ≤ 1.

→Τα πρόσημα των τριγωνομετρικών αριθμών μιας γωνίας ω, ανάλογα με το τεταρτημόριο στο οποίο βρίσκεται η τελική πλευρά της γωνίας αυτής, είναι όπως δείχνει ο παρακάτω πίνακας.

Απάντηση

Κλείσιμο απάντησης

5.Τι είναι το ακτίνιο ή rad;

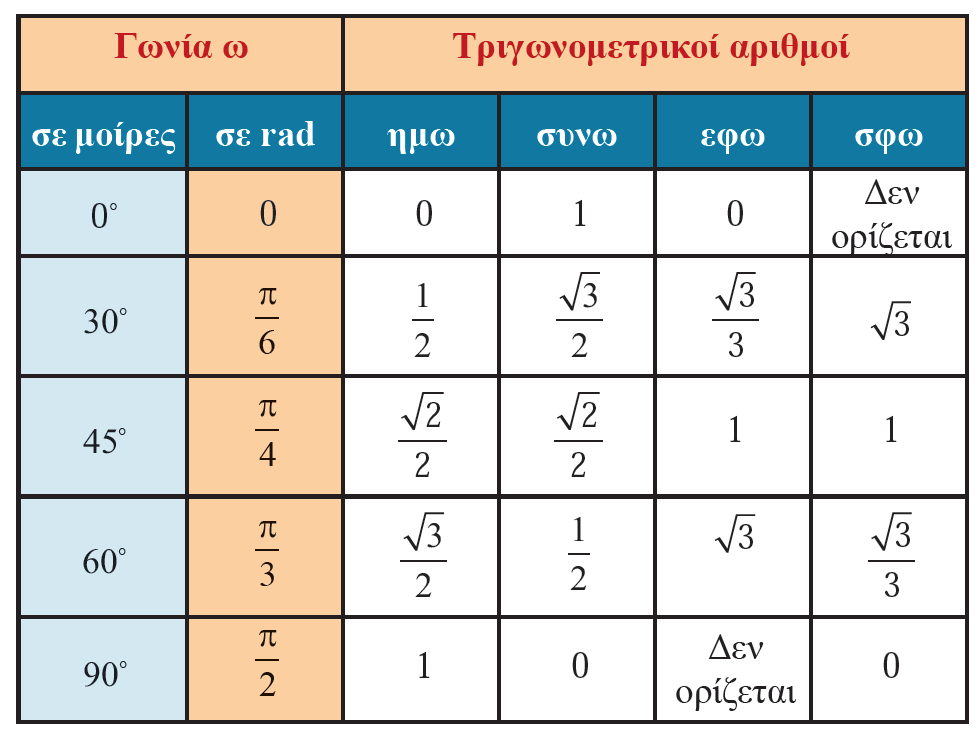
Απάντηση

Ακτίνιο (ή 1 rad ) είναι η γωνία η οποία, όταν γίνει επίκεντρη σε έναν κύκλο, βαίνει σε τόξο ενός ακτινίου (ή 1 rad).

ΣΧΟΛΙΟ

Από τον ορισμό αυτό προκύπτει και η σχέση μοίρας και ακτινίου ως μονάδων μέτρησης γωνιών, ως εξής:
$\large \frac{a}{\pi }=\frac{\mu }{180}$

Στον παρακάτω πίνακα επαναλαμβάνουμε τους τριγωνομετρικούς αριθμούς μερικών γωνιών που είχαμε υπολογίσει στο Γυμνάσιο και οι οποίοι είναι ιδιαίτερα χρήσιμοι στις διάφορες εφαρμογές.

Απάντηση

Κλείσιμο απάντησης

6.Να αποδείξετε ότι για κάθε γωνία ω ισχύει .

Απάντηση

Αν M (x, y) είναι το σημείο στο οποίο η τελική πλευρά της γωνίας ω τέμνει τον τριγωνομετρικό κύκλο, τότε θα είναι x = συνω και y = ημω .

Επειδή όμως (OM) = 1 και (ΟΜ)² = |x|² +|y|² = x² + y² θα ισχύει: x² + y² = 1, οπότε θα έχουμε:

Απάντηση

Κλείσιμο απάντησης

7.Να αποδείξετε ότι για κάθε γωνία ω ισχύει $\large \varepsilon \varphi \omega =\frac{\eta \mu \omega }{\sigma \upsilon \nu \omega }$ και $\large \sigma \varphi \omega =\frac{ \sigma \upsilon \nu \omega}{ \eta \mu \omega}$ .

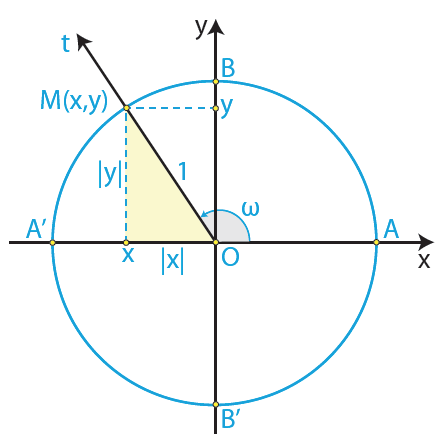
Απάντηση

Αν M (x, y) είναι το σημείο στο οποίο η τελική πλευρά της γωνίας ω τέμνει τον τριγωνομετρικό κύκλο, τότε θα είναι x = συνω και y = ημω , επομένως:
$\large \varepsilon \varphi \omega =\frac{y}{x}=\frac{ \eta \mu \omega}{\sigma \upsilon \nu \omega }$ , (εφόσον x = συνω ≠ 0 ).

$\large \sigma \varphi \omega =\frac{x}{y}=\frac{ \sigma \upsilon \nu \omega}{ \eta \mu \omega}$ , (εφόσον y = ημω ≠ 0 ).

Απάντηση

Κλείσιμο απάντησης

8.Να αποδείξετε ότι για κάθε γωνία ω ισχύει εφω·σφω = 1 .

Απάντηση

Είναι: $\large \varepsilon \varphi \omega =\frac{\eta \mu \omega }{\sigma \upsilon \nu \omega }$ και $\large \sigma \varphi \omega =\frac{ \sigma \upsilon \nu \omega}{ \eta \mu \omega}$ ,(εφόσον συνω ≠ 0 και ημω ≠ 0 ).Επομένως,

$\large \varepsilon \varphi \omega \cdot \sigma \varphi \omega=\frac{ \eta \mu \omega}{\sigma \upsilon \nu \omega }\cdot \frac{ \sigma \upsilon \nu \omega}{ \eta \mu \omega}=1$

Απάντηση

Κλείσιμο απάντησης

9.Να αποδείξετε ότι για κάθε γωνία ω ισχύει: i. $\large \sigma \upsilon \nu ^2\omega =\frac{1}{1+\varepsilon \varphi ^2\omega }$ ii. $\large \eta \mu ^2\omega =\frac{\varepsilon \varphi ^2\omega}{1+\varepsilon \varphi ^2\omega }$ .

Απάντηση

i. Διαιρούμε και τα δύο μέλη της ταυτότητας $\large \eta \mu ^2\omega +\sigma \upsilon \nu ^2\omega =1$ με συν²ω ≠ 0 και έχουμε:

$\frac{\eta \mu ^2\omega}{\sigma \upsilon \nu ^2\omega}+\frac{\sigma \upsilon \nu ^2\omega}{\sigma \upsilon \nu ^2\omega} =\frac{1}{\sigma \upsilon \nu ^2\omega}\Leftrightarrow\varepsilon \varphi ^2\omega+1=\frac{1}{\sigma \upsilon \nu ^2\omega}\Leftrightarrow \sigma \upsilon \nu ^2\omega= \frac{1}{1+\varepsilon \varphi ^2\omega }$ .

Άρα $\large \sigma \upsilon \nu ^2\omega =\frac{1}{1+\varepsilon \varphi ^2\omega }$ .

ii. Αν στην ταυτότητα $\large \eta \mu ^2\omega +\sigma \upsilon \nu ^2\omega =1$ θέσουμε $\large \sigma \upsilon \nu ^2\omega =\frac{1}{1+\varepsilon \varphi ^2\omega }$ έχουμε:

$\eta \mu ^2\omega+\frac{1}{1+\varepsilon \varphi ^2\omega }=1\Leftrightarrow \eta \mu ^2\omega=1-\frac{1}{1+\varepsilon \varphi ^2\omega }\Leftrightarrow\eta \mu ^2\omega= \frac{\varepsilon \varphi ^2\omega}{1+\varepsilon \varphi ^2\omega }$ .

Άρα ^.

Απάντηση

Κλείσιμο απάντησης

10.Τι σχέση έχουν οι τριγωνομετρικοί αριθμοί αντίθετων γωνιών;

Απάντηση

Οι αντίθετες γωνίες έχουν το ίδιο συνημίτονο και αντίθετους τους άλλους τριγωνομετρικούς αριθμούς. Δηλαδή,

$\displaystyle \large \eta \mu (-\omega )=-\eta \mu \omega$ ,

$\displaystyle \large \sigma \upsilon \nu (-\omega )=\sigma \upsilon \nu \omega$ ,

$\displaystyle \large \varepsilon \varphi (-\omega )=-\varepsilon \phi \omega$ ,

$\displaystyle \large \sigma \varphi (-\omega )=-\sigma \phi \omega$ .

Απάντηση

Κλείσιμο απάντησης

11.Τι σχέση έχουν οι τριγωνομετρικοί αριθμοί γωνιών με άθροισμα 180^ο;

Απάντηση

Οι γωνίες με άθροισμα 180^ο έχουν το ίδιο ημίτονο και αντίθετους τους άλλους τριγωνομετρικούς αριθμούς.Δηλαδή,

$\displaystyle \large \eta \mu (180^o-\omega )=\eta \mu \omega$ ,

$\displaystyle \large \sigma \upsilon \nu (180^o-\omega )=-\sigma \upsilon \nu \omega$ ,

$\displaystyle \large \varepsilon \varphi (180^o-\omega )=-\varepsilon \phi \omega$ ,

$\displaystyle \large \sigma \varphi (180^o-\omega )=-\sigma \phi \omega$ .

Απάντηση

Κλείσιμο απάντησης

12.Τι σχέση έχουν οι τριγωνομετρικοί αριθμοί γωνιών που διαφέρουν κατά 180^ο;

Απάντηση

Οι γωνίες που διαφέρουν κατά 180^ο έχουν αντίθετο ημίτονο και συνημίτονο , ενώ έχουν την ίδια εφαπτομένη και συνεφαπτμένη. Δηλαδή,

$\displaystyle \large \eta \mu (180^o+\omega )=-\eta \mu \omega$ ,

$\displaystyle \large \sigma \upsilon \nu (180^o+\omega )=-\sigma \upsilon \nu \omega$ ,

$\displaystyle \large \varepsilon \varphi (180^o+\omega )=\varepsilon \phi \omega$ ,

$\displaystyle \large \sigma \varphi (180^o+\omega )=\sigma \phi \omega$ .

Απάντηση

Κλείσιμο απάντησης

13.Τι σχέση έχουν οι τριγωνομετρικοί αριθμοί γωνιών με άθροισμα 90^ο;

Απάντηση

Αν δύο γωνίες έχουν άθρισμα 90ο , τότε το ημίτονο της μιας ισούται με το συνημίτονο της άλλης και η εφαπτομένη της μιας ισούται με τη συνεφαπτομένη της άλλης. Δηλαδή,

$\displaystyle \large \eta \mu (90^o-\omega )=\sigma \upsilon \nu \omega$ ,

$\displaystyle \large \sigma \upsilon \nu (90^o-\omega )=\eta \mu\omega$ ,

$\displaystyle \large \varepsilon \varphi (90^o-\omega )=\sigma \phi \omega$ ,

$\displaystyle \large \sigma \varphi (90^o-\omega )=\varepsilon \phi \omega$ .

ΣΧΟΛΙΟ

Αναγωγή στο πρώτο τεταρτημόριο

Απάντηση

Κλείσιμο απάντησης

14.Πότε μια συνάρτηση f με πεδίο ορισμού Α λέγεται περιοδική;

Απάντηση

Μία συνάρτηση f με πεδίο ορισμού το Α λέγεται περιοδική, όταν υπάρχει πραγματικός αριθμός Τ > 0 τέτοιος, ώστε για κάθε x ∈A να ισχύει:

i. x+T ∈A, x-T ∈A και ii. f(x + T) = f(x – T) = f(x) .

ΣΧΟΛΙΟ

Ο πραγματικός αριθμός Τ λέγεται περίoδoς της συνάρτησης f.

Απάντηση

Κλείσιμο απάντησης

15.Nα μελετήσετε τη συνάρτηση f(x) = ημx .

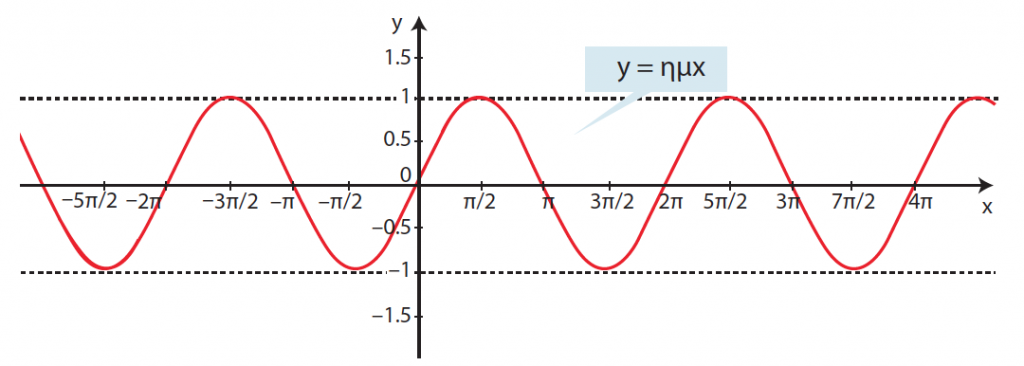
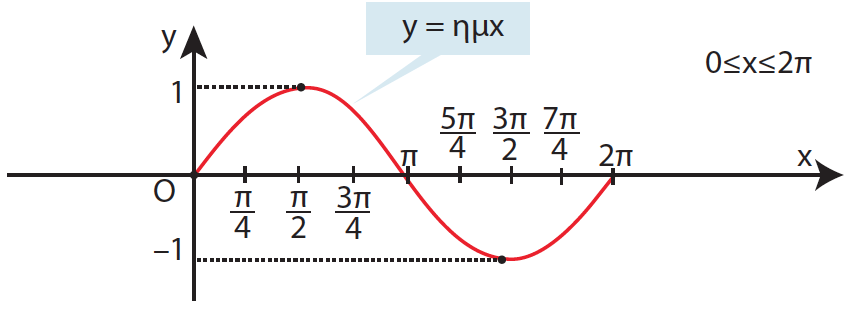
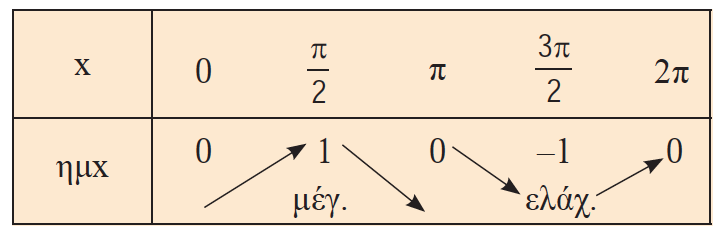
Απάντηση

Η συνάρτηση ημίτονο είναι μια αντιστοιχία όπου κάθε πραγματικός αριθμός x αντιστοιχίζεται στο ημx (rad).

Η συνάρτηση ημίτονο είναι περιοδική με ελάχιστη θετική περίοδο το 2π.

Είναι δηλ. ημ(x + 2π) = ημ(x – 2π) = ημx για κάθε x∈ℝ .

Το πεδίο ορισμού της f(x) = ημx είναι το (−∞, +∞ ) δηλ το ℝ ,ενώ το σύνολο τιμών της συνάρτησης είναι το [−1,1] αφού −1 ≤ ηµx ≤ 1 για κάθε x∈ℝ.

Η γραφική παράσταση της συνάρτησης λέγεται ημιτονοειδής καμπύλη.

Η συνάρτηση ημίτονο είναι περιττή συνάρτηση αφού ηµ (−x) = −ηµx για κάθε x∈ℝ.

Μονοτονία της f(x) = ημx στο [0, 2π].

Η f(x) = ημx είναι γνησίως αύξουσα για κάθε x∈[ 0 , $\displaystyle \frac{\pi }{2}$ ] .

Η f(x) = ημx είναι γνησίως φθίνουσα για κάθε x∈[ $\displaystyle \frac{\pi }{2}$ , $\displaystyle \frac{3\pi }{2}$ ] .

Η f(x) = ημx είναι γνησίως αύξουσα για κάθε x∈[ $\displaystyle \frac{3\pi }{2}$ , 2π ] .

Ακρότατα της f(x) = ημx στο [0, 2π] .

Η f(x) = ημx παρουσιάζει μέγιστο για x = $\displaystyle \frac{\pi }{2}$ το $\displaystyle f(\frac{\pi }{2})=\eta \mu \frac{\pi }{2}=1$ .

Η f(x) = ημx παρουσιάζει ελάχιστο για x = $\displaystyle \frac{3\pi }{2}$ το $\displaystyle f(\frac{3\pi }{2})=\eta \mu \frac{3\pi }{2}=-1$ .

Απάντηση

Κλείσιμο απάντησης

16.Nα μελετήσετε τη συνάρτηση f(x) = συνx .

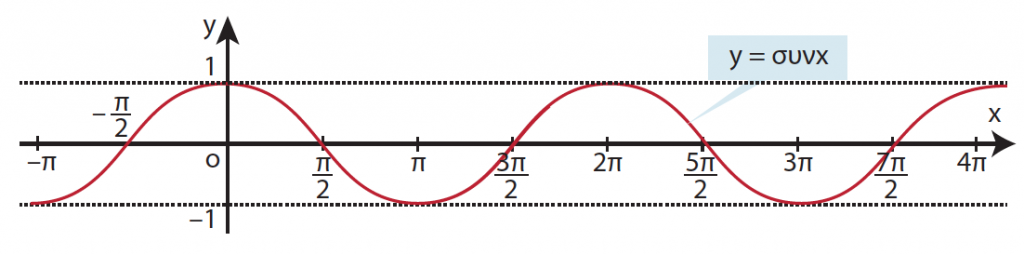
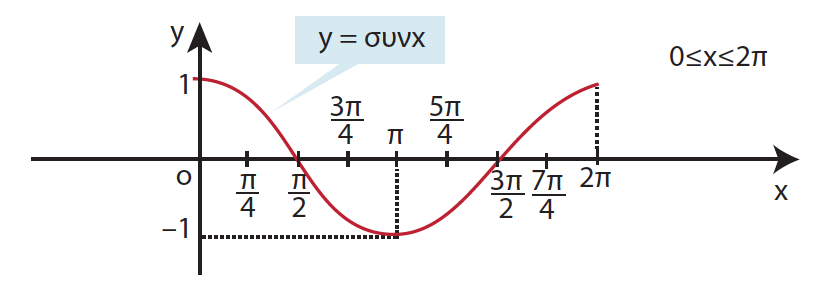
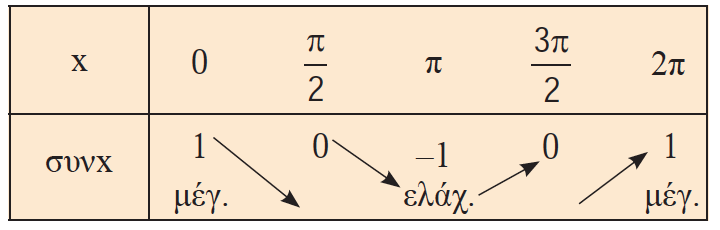
Απάντηση

Η συνάρτηση συνημίτονο είναι μια αντιστοιχία όπου κάθε πραγματικός αριθμός x αντιστοιχίζεται στο συνx (rad).

Η συνάρτηση συνημίτονο είναι περιοδική με ελάχιστη θετική περίοδο το 2π.

Είναι δηλ. συν(x + 2π) = συν(x – 2π) = συνx για κάθε x∈ℝ .

Το πεδίο ορισμού της f(x) = συνx είναι το (−∞, +∞ ) δηλ το ℝ ,ενώ το σύνολο τιμών της συνάρτησης είναι το [−1,1] αφού −1 ≤ συνx ≤ 1 για κάθε x∈ℝ.

Η γραφική παράσταση της συνάρτησης λέγεται συνημιτονοειδής καμπύλη.

Η συνάρτηση συνημίτονο είναι άρτια συνάρτηση αφού συν (−x) = συνx για κάθε x∈ℝ.

Μονοτονία της f(x) = συνx στο [0, 2π].

Η f(x) = συνx είναι γνησίως φθίνουσα για κάθε x∈[0 , π] .

Η f(x) = συνx είναι γνησίως αύξουσα για κάθε x∈[π , 2π] .

Ακρότατα της f(x) = συνx στο [0, 2π] .

Η f(x) = συνx παρουσιάζει μέγιστο για x = 0 και για x = 2π το f(0) = συν0 =f(2π) =συν2π = 1 .

Η f(x) = συνx παρουσιάζει ελάχιστο για x = π το f(π) = συνπ = -1 .

Απάντηση

Κλείσιμο απάντησης

17.Nα μελετήσετε τη συνάρτηση f(x) = εφx .

Απάντηση

Το πεδίο ορισμού της f(x) = εφx είναι το Α={x∈ℝ |συνx ≠ 0} καθώς $\displaystyle \varepsilon \varphi x=\frac{\eta \mu x}{\sigma \upsilon \nu x}$ .

Το σύνολο τιμών της f(x) = εφx είναι όλο το ℝ.

Η συνάρτηση f(x) = εφx είναι περιοδική με ελάχιστη θετική περίοδο το π.

Είναι δηλ. εφ(x + π) = εφ(x – π) = εφx για κάθε x∈ℝ με $\displaystyle x\neq \kappa \pi +\frac{\pi }{2},\kappa \epsilon \mathbb{Z}$ .

Αρκούμαστε λοιπόν να τη μελετήσουμε στο διάστημα $\displaystyle (-\frac{\pi }{2},\frac{\pi }{2})$ .

Η συνάρτηση εφαπτομένη είναι περιττή συνάρτηση αφού εφ(−x) = εφx για κάθε x∈Α ={x∈ℝ|συνx ≠0}.

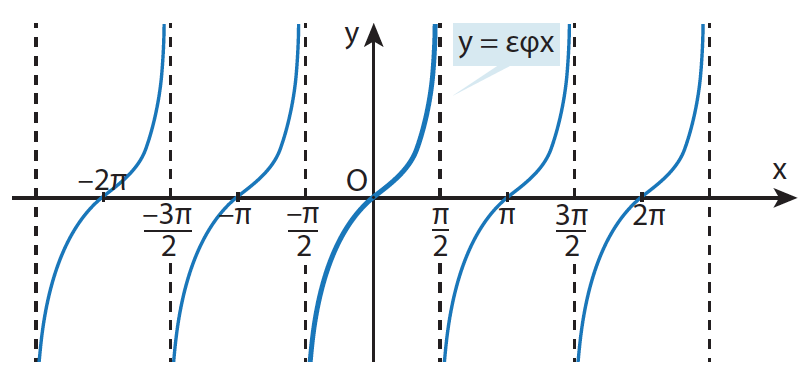
Οι ευθείες της μορφής $\displaystyle x=\kappa \pi +\frac{\pi }{2},\kappa \epsilon \mathbb{Z}$ λέγονται κατακόρυφες ασύμπτωτες της γραφικής παράστασης της f.

Μονοτονία της f(x) = εφx στο $\displaystyle (-\frac{\pi }{2},\frac{\pi }{2})$ .

Η f(x) = εφx είναι γνησίως αύξουσα για κάθε x∈ $\displaystyle (-\frac{\pi }{2},\frac{\pi }{2})$ και επομένως δεν παρουσιάζει ακρότατα.

Απάντηση

Κλείσιμο απάντησης

18.Tι γνωρίζετε για τις συναρτήσεις f(x) = ρημ(ωx) και g(x) = ρσυν(ωx);

Απάντηση

Οι συναρτήσεις f(x) = ρημ(ωx) και g(x) = ρσυν(ωx), με ρ,ω > 0, έχουν πεδίο ορισμού το ℝ, περίοδο $\displaystyle T=\frac{2\pi }{\omega }$ ,μέγιστη τιμή ρ, ελάχιστη τιμή -ρ και σύνολο τιμών [-ρ , ρ].

Απάντηση

Κλείσιμο απάντησης

19.Να λύσετε την εξίσωση ημx = α .

Απάντηση

Αν θ είναι μία λύση της εξίσωσης ημx = α, αν δηλαδή ισχύει ημθ = α, τότε οι λύσεις της εξίσωσης δίνονται από τους τύπους:
$\eta \mu x=\eta \mu \vartheta \Leftrightarrow\left\{\begin{matrix}x=2\kappa \pi +\theta \\ \eta '\\ x=2\kappa \pi +(\pi -\theta)\end{matrix}\right. ,\kappa \epsilon \mathbb{Z}$

Απάντηση

Κλείσιμο απάντησης

20.Να λύσετε την εξίσωση συνx = α .

Απάντηση

Αν θ είναι μία λύση της εξίσωσης συνx = α, αν δηλαδή ισχύει συνθ = α, τότε οι λύσεις της εξίσωσης δίνονται από τους τύπους:
$\sigma \upsilon \nu x=\sigma \upsilon \nu \vartheta \Leftrightarrow x=2\kappa \pi \pm \theta ,\kappa \epsilon \mathbb{Z}$

Απάντηση

Κλείσιμο απάντησης

21.Να λύσετε την εξίσωση εφx = α .

Απάντηση

Αν θ είναι μια λύση της εξίσωσης εφx = α, αν δηλαδή ισχύει εφx = εφθ, τότε οι λύσεις της εξίσωσης αυτής είναι:
$\varepsilon \varphi x= \varepsilon \varphi \theta \Leftrightarrow x=\kappa \pi + \theta ,\kappa \epsilon \mathbb{Z}$

Απάντηση

Κλείσιμο απάντησης

22.Να λύσετε την εξίσωση σφx = α .

Απάντηση

Αν θ είναι μια λύση της εξίσωσης σφx = α, αν δηλαδή ισχύει σφx = σφθ, τότε οι λύσεις της εξίσωσης αυτής είναι:
$\sigma \varphi x= \sigma \varphi \theta \Leftrightarrow x=\kappa \pi + \theta ,\kappa \epsilon \mathbb{Z}$

Απάντηση

Κλείσιμο απάντησης

23.Τριγωνομετρικοί αριθμοί αθροίσματος γωνιών .

Απάντηση

συν(α–β) = συνασυνβ + ημαημβ

συν(α+β) = συνασυνβ – ημαημβ

ημ(α+β) = ημασυνβ + συναημβ

ημ(α-β) = ημασυνβ – συναημβ

$\varepsilon \varphi (\alpha +\beta )=\frac{\varepsilon \phi \alpha +\varepsilon \phi \beta }{1-\varepsilon \phi \alpha \cdot \varepsilon \phi \beta}$

$\varepsilon \varphi (\alpha -\beta )=\frac{\varepsilon \phi \alpha -\varepsilon \phi \beta }{1+\varepsilon \phi \alpha \cdot \varepsilon \phi \beta}$

$\sigma \varphi (\alpha +\beta )=\frac{\sigma \phi \alpha \cdot \sigma \phi \beta-1 }{\sigma \phi \beta +\sigma \phi a}$

$\sigma \varphi (\alpha -\beta )=\frac{\sigma \phi \alpha \cdot \sigma \phi \beta+1 }{\sigma \phi \beta -\sigma \phi a}$

Απάντηση

Κλείσιμο απάντησης

24.Τριγωνομετρικοί αριθμοί της γωνίας 2α .

Απάντηση

ημ2α = 2ημασυνα

συν2α = συν²α – ημ²α = 2συν²α -1 = 1 – 2ημ²α

$\varepsilon \varphi 2\alpha =\frac{2\varepsilon \varphi a}{1-\varepsilon \varphi ^2\alpha }$

Απάντηση

Κλείσιμο απάντησης

25.Tύποι αποτετραγωνισμού.

Απάντηση
$\eta \mu ^2a=\frac{1-\sigma \upsilon \nu 2\alpha}{2},\sigma \upsilon \nu ^2a=\frac{1+\sigma \upsilon \nu 2\alpha}{2},\varepsilon \varphi ^2\alpha =\frac{1-\sigma \upsilon \nu 2\alpha }{1+\sigma \upsilon \nu 2\alpha }$

Απάντηση

Κλείσιμο απάντησης

Pages: 1 2 3 4 5

error: Alert: Content is protected !!