Εκθετική και Λογαριθμική συνάρτηση
Απάντηση Av α>0, μ ακέραιος και ν θετικός ακέραιος, τότε ορίζουμε: επιπλέον, αν μ, ν, θετικοί ακέραιοι, ορίζουμε Αν α, β είναι θετικοί πραγματικοί αριθμοί και x, x1, x2 ∈ℝ, τότε:
και
,
.
Απάντηση Έστω α > 0 ,τότε αντιστοιχίζοντας το πραγματικό x στη δύναμη αx ,ορίζουμε τη συνάρτηση f: ℝ → ℝ με f(x) = αx ,που όταν α≠1 λέγεται εκθετική συνάρτηση με βάση α. ΣΧΟΛΙΟ Αν α = 1 τότε έχουμε τη σταθερή συνάρτηση f(x) = 1.
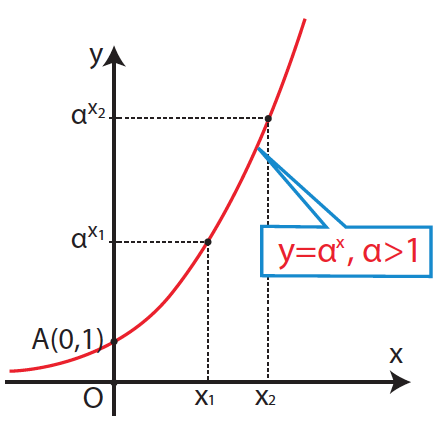
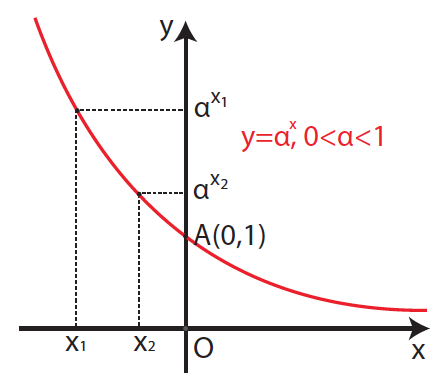
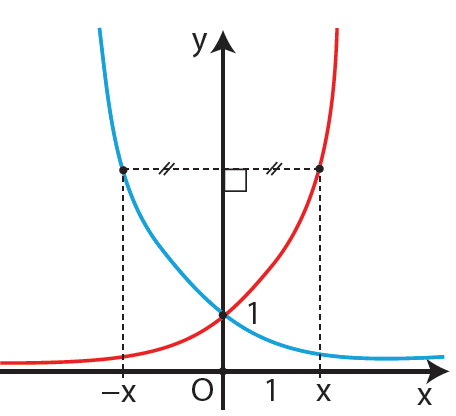
Απάντηση Το πεδίο ορισμού της f(x) = αx είναι το (−∞, +∞ ) δηλ το ℝ . Το σύνολο τιμών της συνάρτησης είναι το (0, +∞). Η γραφική παράσταση της f(x) = αx τέμνει τον y’y άξονα στο σημείο Α(0,1). Η εκθετική συνάρτηση f(x) = αx είναι « ένα προς ένα » στο ℝ , δηλ για κάθε x1,x2 ∈ ℝ ισχύει: x1 ≠ x2 ⇔ αx1 ≠ αx2 ή ισοδύναμα αx1 = αx2 ⇔ x1 = x2 . (Η ιδιότητα αυτή είναι ιδιαίτερα χρήσιμη για την επίλυση εξισώσεων, όπου ο άγνωστος εμφανίζεται στον εκθέτη. Οι εξισώσεις αυτές λέγονται εκθετικές εξισώσεις.) Η γραφική παράσταση της f(x) = αx βρίσκεται πάντα πάνω από τον x’x άξονα. Όταν f(x) = αx ,α > 1 Είναι γνησίως αύξουσα στο ℝ , δηλ για κάθε x1,x2 ∈ ℝ ισχύει: x1 < x2 ⇔ αx1 < αx2 . Έχει οριζόντια ασύμπτωτη τον x’x άξονα στο −∞. Όταν f(x) = αx , 0 < α < 1 Είναι γνησίως φθίνουσα στο ℝ , δηλ για κάθε x1,x2 ∈ ℝ ισχύει: x1 < x2 ⇔ αx1 > αx2 . Έχει οριζόντια ασύμπτωτη τον x’x άξονα στο +∞. ΣΧΟΛΙΟ Οι γραφικές παραστάσεις των συναρτήσεων f1(x) = αx ,α > 1 και f2(x) = αx , 0 < α < 1 είναι συμμετρικές ως προς τον y’y άξονα. →Το σύμβολο e παριστάνει τον άρρητο αριθμό 2,71828….
Απάντηση Μία ακόμη εκθετική συνάρτηση με βάση το e είναι η Q(t) = Q0·ect . Αυτή εκφράζει ένα φυσικό μέγεθος, που μεταβάλλεται με το χρόνο t. To Q0 είναι η αρχική τιμή του Q (για t = 0) και είναι Q0 > 0, ενώ το c είναι μια σταθερά που εξαρτάται κάθε φορά από τη συγκεκριμένη εφαρμογή. Η συνάρτηση αυτή είναι γνωστή ως νόμος της εκθετικής μεταβολής. Αν c > 0 η συνάρτηση Q είναι γνησίως αύξουσα και εκφράζει το νόμο της εκθετικής αύξησης, ενώ αν c < 0 η Q είναι γνησίως φθίνουσα και εκφράζει το νόμο της εκθετικής απόσβεσης. Ο νόμος της εκθετικής μεταβολής αποτελεί ένα ικανοποιητικό μοντέλο για πάρα πολλές εφαρμογές της Φυσικής, της Βιολογίας, της Στατιστικής και άλλων επιστημών.
Απάντηση Λογάριθμο του αριθμού θ > 0, με βάση α , 0 < α ≠ 1, θα ονομάζουμε τον πραγματικό αριθμό x, τον οποίο πρέπει να υψώσουμε στη βάση α ώστε να μας δώσει τον θετικό αριθμό θ. Ισχύει, δηλαδή, η ισοδυναμία: αx = θ ⇔ x = logα θ . ΣΧΟΛΙΑ Από τον ορισμό προκύπτουν άμεσα οι παρακάτω ισότητες: logα αx = x αlogαθ = θ logα 1 = 0 logα α = 1 Ειδικότερα, αν έχουμε για βάση το 10 ονομάζουμε το λογάριθμο δεκαδικό και γράφουμε logθ αντί για log10θ. Δηλαδή: log θ = x ⇔ 10x = θ , ενώ αν έχουμε για βάση τον αριθμό e ( ≅ 2,71828) ονομάζουμε το λογάριθμο φυσικό ή νεπέριο και γράφουμε lnθ αντί για logeθ. Δηλαδή: ln θ = x ⇔ ex = θ .
Απάντηση Εστω ότι είναι: logα θ1 = x1 και logα θ2 = x2 . (1) Τότε έχουμε αx1 = θ1 και αx2 = θ2 , οπότε αx1·αx2 = θ1·θ2 και αx1+x2 = θ1·θ2 . Από τον ορισμό όμως του λογάριθμου, η τελευταία ισότητα είναι ισοδύναμη με την : logα (θ1·θ2) = x1 + x2 από την οποία, λόγω των (1), έχουμε τελικά: logα (θ1·θ2) = logα θ1 + logα θ2 . ΣΧΟΛΙΟ Με τον ίδιο ακριβώς τρόπο αποδεικνύουμε την παρακάτω ιδιότητα: logα (
) = logα θ1 – logα θ2 .
Απάντηση Έστω ότι είναι: logα θ = x . (2) Τότε έχουμε αx = θ οπότε: ακ·x = θκ . Από τον ορισμό όμως του λογάριθμου, η τελευταία ισότητα είναι ισοδύναμη με την logα θκ = κ·x από την οποία, λόγω της (2), προκύπτει ότι: logα θκ = κ·logα θ .
Απάντηση Αν α, β >0 με α , β ≠ 1 , τότε για κάθε θ > 0 ισχύει:
.
Απάντηση Έστω 0 < α ≠ 1 ,τότε αντιστοιχίζοντας το θετικό αριθμό x στον λογάριθμο logαx ,ορίζουμε τη συνάρτηση f: (0, +∞) → ℝ με f(x) = logαx ,που λέγεται λογαριθμική συνάρτηση με βάση α. ΣΧΟΛΙΟ Οι γραφικές παραστάσεις των συναρτήσεων y = logαx και y = αx, είναι συμμετρικές ως προς την ευθεία που διχοτομεί τις γωνίες xÔy και x΄Ôy΄.
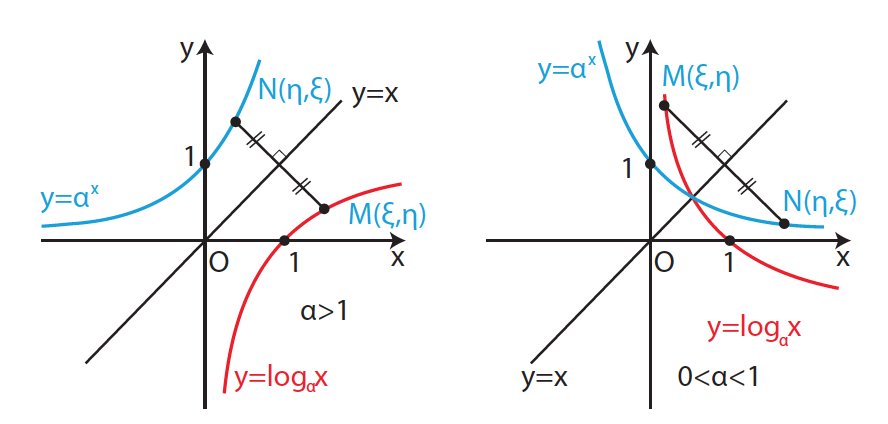
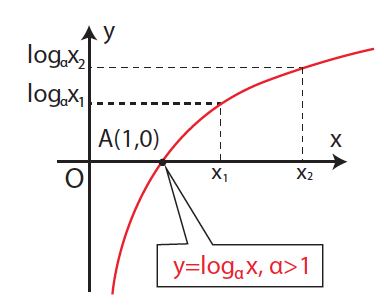
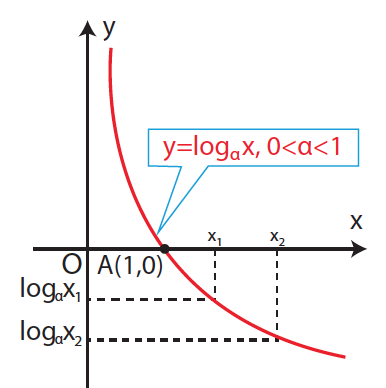
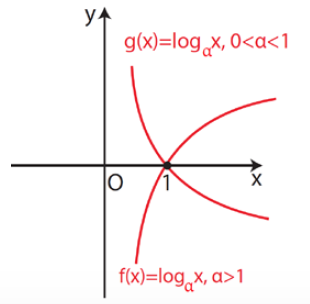
Απάντηση Το πεδίο ορισμού της f(x) = logαx είναι το (0, +∞) . Η γραφική παράσταση της f(x) = logαx τέμνει τον x’x άξονα στο σημείο Α(1,0). H συνάρτηση είναι « ένα προς ένα » στο (0, +∞) , δηλ για κάθε x1,x2 ∈(0, +∞) ισχύει: x1 ≠ x2 ⇔ logαx1 ≠ logαx2 ή ισοδύναμα logαx1 = logαx2 ⇔ x1 = x2 . Όταν f(x) = logαx ,α > 1 Είναι γνησίως αύξουσα στο (0, +∞) , δηλ για κάθε x1,x2 ∈(0, +∞) ισχύει : x1 < x2 ⇔ logαx1 < logαx2. Η γραφική παράσταση της f(x) = logαx έχει κατακόρυφη ασύμπτωτη τον Οy΄ ημιάξονα. Όταν f(x) = logαx ,0 < α < 1 Είναι γνησίως φθίνουσα στο (0, +∞) , δηλ για κάθε x1,x2 ∈(0, +∞) ισχύει : x1 < x2 ⇔ logαx1 > logαx2. Η γραφική παράσταση της f(x) = logαx έχει κατακόρυφη ασύμπτωτη τον Οy ημιάξονα. ΣΧΟΛΙΟ Οι γραφικές παραστάσεις των συναρτήσεων f(x) = logαx ,α > 1και g(x) = logαx , 0< α < 1 είναι συμμετρικές ως προς τον x’x άξονα.
Το σύνολο τιμών της συνάρτησης είναι το (−∞, +∞ ) δηλ το ℝ.