Τρίγωνα
1.Πότε ένα τρίγωνο λέγεται σκαληνό; Απάντηση Ένα τρίγωνο λέγεται σκαληνό όταν έχει όλες τις πλευρές του άνισες.

2.Πότε ένα τρίγωνο λέγεται ισοσκελές; Απάντηση Ένα τρίγωνο λέγεται ισοσκελές όταν έχει δύο πλευρές του ίσες. Σε ένα ισοσκελές τρίγωνο ΑΒΓ με ΑΒ = ΑΓ η πλευρά ΒΓ λέγεται βάση του και το σημέιο Α κορυφή του.

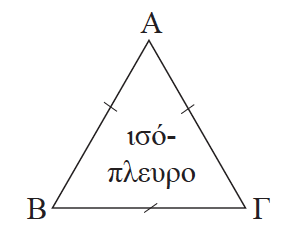
3.Πότε ένα τρίγωνο λέγεται ισόπλευρο; Απάντηση Ένα τρίγωνο λέγεται ισόπλευρο όταν έχει όλες τις πλευρές του ίσες.
4.Πότε ένα τρίγωνο λέγεται οξυγώνιο; Απάντηση Ένα τρίγωνο λέγεται οξυγώνιο όταν έχει όλες τις γωνίες του οξείες .

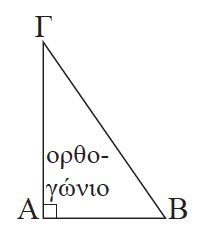
5.Πότε ένα τρίγωνο λέγεται ορθογώνιο; Απάντηση Ένα τρίγωνο λέγεται ορθογώνιο όταν έχει μια γωνία ορθή . Σε ένα ορθογώνιο τρίγωνο η πλευρά που βρίσκεται απέναντι από την ορθή γωνία λέγεται υποτείνουσα και οι άλλες δύο λέγονται κάθετες πλευρές του τριγώνου.
6.Πότε ένα τρίγωνο λέγεται αμβλυγώνιο; Απάντηση Ένα τρίγωνο λέγεται αμβλυγώνιο όταν έχει μια γωνία αμβλεία.
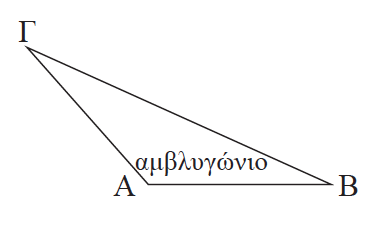
Απάντηση Διάμεσος ενός τριγώνου λέγεται το ευθύγραμμο τμήμα που ενώνει μια κορυφή με το μέσο της απέναντι πλευράς. Η διάμεσος που αντιστοιχεί στην πλευρά α του τριγώνου ΑΒΓ συμβολίζεται με μα, ενώ οι διάμεσοι που αντιστοιχούν στις πλευρές β και γ συμβολίζονται με μβ και μγ αντίστοιχα.
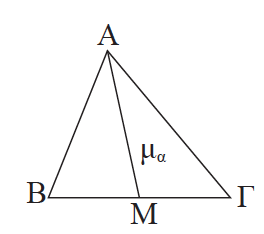
8.Τι ονομάζουμε διχοτόμο μιας γωνίας ενός τριγώνου; Απάντηση
Διχοτόμος μιας γωνίας ενός τριγώνου λέγεται το ευθύγραμμο τμήμα της διχοτόμου της γωνίας, από την κορυφή της μέχρι την απέναντι πλευρά. Η διχοτόμος της γωνίας Â του τριγώνου ΑΒΓ συμβολίζεται με δα, ενώ διχοτόμοι των γωνιών B̂ και Γ̂ του τριγώνου συμβολίζονται με δβ και δγ αντίστοιχα.
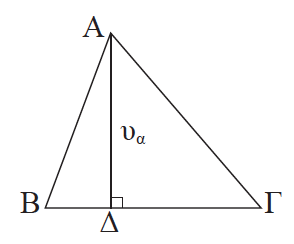
9.Τι ονομάζουμε ύψος ενός τριγώνου; Απάντηση Ύψος τριγώνου λέγεται το κάθετο ευθύγραμμο τμήμα, που φέρεται από μια κορυφή προς την ευθεία της απέναντι πλευράς. Τα ύψη που φέρονται από τις κορυφές Α, Β και Γ συμβολίζονται αντίστοιχα με υα, υβ και υγ. ΣΧΟΛΙΟ Το ΑΔ είναι το ύψος από την κορυφή Α. Το σημείο Δ λέγεται προβολή του Α πάνω στην ευθεία ΒΓ ή και ίχνος της καθέτου, που φέρεται από το Α στην ευθεία ΒΓ. Οι διάμεσοι, οι διχοτόμοι και τα ύψη ενός τριγώνου λέγονται δευτερεύοντα στοιχεία του.
10.Να αναφέρετε τα κριτήρια ισότητας τριγώνων. Απάντηση Αν δύο τρίγωνα έχουν δύο πλευρές ίσες μία προς μία και τις περιεχόμενες σε αυτές γωνίες ίσες, τότε είναι ίσα.(Π-Γ-Π) Αν δύο τρίγωνα έχουν μια πλευρά και τις προσκείμενες σε αυτή γωνίες ίσες μία προς μία, τότε τα τρίγωνα είναι ίσα.(Γ-Π-Γ) Αν δύο τρίγωνα έχουν τις πλευρές τους ίσες μία προς μία, τότε τα τρίγωνα είναι ίσα.(Π-Π-Π) ΣΧΟΛΙΟ Δύο τρίγωνα, είναι ίσα αν μετά από κατάλληλη μετατόπιση ταυτίζονται. Δύο ίσα τρίγωνα έχουν τις πλευρές τους και τις γωνίες τους ίσες μία προς μία. Σε δύο ίσα τρίγωνα απέναντι από ίσες πλευρές βρίσκονται ίσες γωνίες και αντίστροφα. Οι ίσες πλευρές που βρίσκονται απέναντι από ίσες γωνίες λέγονται αντίστοιχες ή ομόλογες. H ισότητα τριγώνων είναι η βασική μέθοδος για την απόδειξη της ισότητας τμημάτων ή γωνιών.
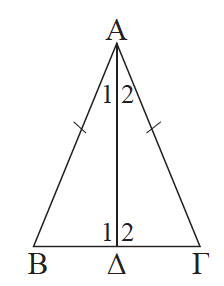
Απάντηση i. Έστω ισοσκελές τρίγωνο ΑΒΓ με ΑΒ = ΑΓ. Φέρουμε τη διχοτόμο του ΑΔ. Τα τρίγωνα ΑΔΒ και ΑΔΓ έχουν ΑΒ = ΑΓ, ΑΔ κοινή και Â1 = Â2 (ΠΓΠ), επομένως είναι ίσα, οπότε B̂ = Γ̂ . ii. Από την ίδια ισότητα τριγώνων προκύπτει ότι ΒΔ = ΔΓ, οπότε η ΑΔ είναι διάμεσος και Δ̂ 1 = Δ̂ 2. Από την τελευταία ισότητα και επειδή Δ̂ 1 + Δ̂ 2 = 180° προκύπτει ότι Δ̂ 1 = Δ̂ 2 = 90°, οπότε συμπεραίνουμε ότι το ΑΔ είναι ύψος του τριγώνου. ΠΟΡΙΣΜΑ Οι γωνίες ισόπλευρου τριγώνου είναι ίσες.
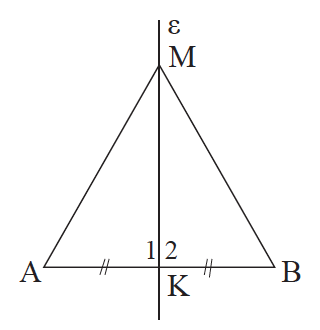
12.Να αποδείξετε οτι κάθε σημείο της μεσοκαθέτου ενός ευθύγραμμου τμήματος ισαπέχει από τα άκρα του. Απάντηση Έστω ε η μεσοκάθετος ενός τμήματος ΑΒ και Μ ένα σημείο της. Τα τρίγωνα ΜΚΑ και ΜΚΒ έχουν ΚΑ = ΚΒ, ΜΚ κοινή και Κ1 = K2 = 90° (ΠΓΠ), επομένως είναι ίσα, οπότε ΜΑ = ΜΒ.
13.Να αποδείξετε οτι αν δύο τόξα ενός κύκλου είναι ίσα, τότε και οι χορδές τους είναι ίσες. Απάντηση Έστω AB και ΓΔ δύο ίσα τόξα ενός κύκλου (Ο, ρ) . Τότε είναι ΑÔΒ = ΓÔΔ. Τα τρίγωνα ΟΑΒ και ΟΓΔ έχουν ΟΑ = ΟΓ = ρ, ΟΒ = ΟΔ = ρ και ΑÔΒ = ΓÔΔ. Επομένως είναι ίσα, οπότε ΑΒ = ΓΔ.

14.Να αποδείξετε οτι η διάμεσος ισοσκελούς τριγώνου, που αντιστοιχεί στη βάση του, είναι διχοτόμος και ύψος. Απάντηση Έστω ισοσκελές τρίγωνο ΑΒΓ με ΑΒ = ΑΓ και ΑΔ η διάμεσός του . Τα τρίγωνα ΑΒΔ και ΑΓΔ έχουν ΑΒ = ΑΓ, ΑΔ κοινή και ΒΔ = ΔΓ, άρα (ΠΠΠ) είναι ίσα, οπότε Â1 = Â2, και Δ̂ 1 = Δ̂ 2. Από τις ισότητες αυτές προκύπτει αντίστοιχα ότι η ΑΔ είναι διχοτόμος και ύψος.

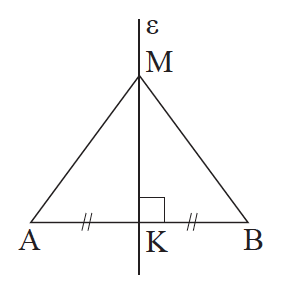
15.Να αποδείξετε οτι κάθε σημείο που ισαπέχει από τα άκρα ενός τμήματος ανήκει στη μεσοκάθετό του. Απάντηση Έστω ευθύγραμμο τμήμα ΑΒ , Μ ένα σημείο, ώστε ΜΑ = ΜΒ και Κ το μέσο του ΑΒ. Τότε το τρίγωνο ΑΜΒ είναι ισοσκελές και η ΜΚ διάμεσός του, οπότε, σύμφωνα με το προηγούμενο πόρισμα, η ΜΚ θα είναι και ύψος, δηλαδή η ΜΚ είναι μεσοκάθετος του ΑΒ.
16.Να αποδείξετε οτι αν οι χορδές δύο τόξων ενός κύκλου, μικρότερων του ημικυκλίου, είναι ίσες, τότε και τα τόξα είναι ίσα. Απάντηση Έστω δύο τόξα AB και ΓΔ ενός κύκλου (Ο, ρ) μικρότερα του ημικυκλίου, με ΑΒ = ΓΔ. Τότε τα τρίγωνα ΟΑΒ και ΟΓΔ έχουν: ΟΑ = ΟΓ = ρ, ΟΒ = ΟΔ = ρ και ΑΒ = ΓΔ, άρα (ΠΠΠ) είναι ίσα. Επομένως, ΑÔΒ = ΓÔΔ, οπότε AB = ΓΔ. ΣΧΟΛΙΟ Αν οι χορδές δύο τόξων ενός κύκλου μεγαλύτερων του ημικυκλίου είναι ίσες, τότε και τα τόξα είναι ίσα. Για να κατασκευάσουμε ίσα τόξα πάνω σε έναν κύκλο ή σε ίσους κύκλους αρκεί να πάρουμε, με το διαβήτη, ίσες χορδές.

Απάντηση Έστω ευθεία xʹx, σημείο Α εκτός αυτής και σημείο Μ της xʹx . Αν η ΑΜ είναι κάθετη στην xʹx, τότε το θεώρημα ισχύει ως προς την ύπαρξη της καθέτου. Έστω ότι η ΑΜ δεν είναι κάθετη στην xʹx. Στο ημιεπίπεδο που ορίζει η xʹx και δεν περιέχει το Α θεωρούμε την ημιευθεία Μy, ώστε να είναι xM̂ y = AM̂ x και πάνω σε αυτή σημείο Β, ώστε ΜΑ = ΜΒ. Επειδή τα σημεία Α, Β είναι εκατέρωθεν της xʹx, η xʹx τέμνει την ΑΒ σε ένα εσωτερικό σημείο, έστω Κ. Αφού ΜΑ = ΜΒ και M1 = M2, η ΜΚ είναι διχοτόμος στο ισοσκελές τρίγωνο ΜΑΒ, άρα είναι και ύψος και επομένως ΑΒ⊥xʹx. Έστω ότι υπάρχει και άλλη ευθεία ΑΛ κάθετη στην xʹx . Τότε τα τρίγωνα ΑΜΛ και ΒΜΛ είναι ίσα, γιατί έχουν ΜΛ κοινή, ΜΑ = ΜΒ και M1 = M2, οπότε θα είναι και Λ 1 = Λ 2. Όμως Λ 1= 90°, άρα και Λ 2 = 90°, οπότε Λ 1 + Λ 2 = 180° το οποίο σημαίνει ότι τα σημεία Α, Λ, Β είναι συνευθειακά, δηλαδή η ΑΛ ταυτίζεται με την ΑΚ, που είναι άτοπο.

18.Να αναφέρετε συνοπτικά πότε δυο ορθογώνια τρίγωνα είναι μεταξύ τους ίσα. Απάντηση Δύο ορθογώνια τρίγωνα είναι ίσα, όταν έχουν: ΣΧΟΛΙΟ Το ύψος ισοσκελούς τριγώνου που αντιστοιχεί στη βάση είναι διάμεσος και διχοτόμος της γωνίας της κορυφής.
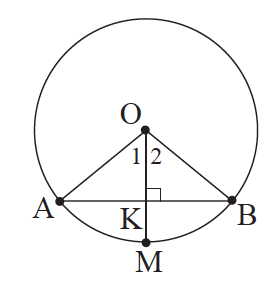
Απάντηση Ας θεωρήσουμε έναν κύκλο (Ο, ρ), μια χορδή του ΑΒ και την κάθετη ΟΚ της ΑΒ, που τέμνει τον κύκλο στο σημείο Μ . Επειδή το τμήμα ΟΚ είναι ύψος στο ισοσκελές τρίγωνο ΟΑΒ (ΟΑ = ΟΒ = ρ), σύμφωνα με το προηγούμενο πόρισμα είναι διάμεσος και διχοτόμος, δηλαδή το Κ είναι μέσο του ΑΒ και Ô1 = Ô2. Αφού Ô1 = Ô2 προκύπτει ότι AΜ = MB.
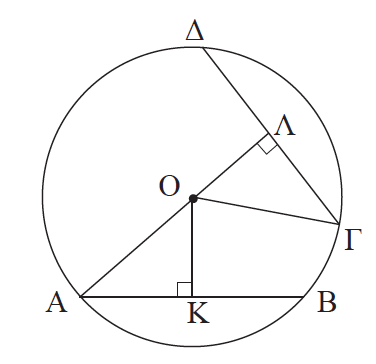
Απάντηση ʹΕστω οι ίσες χορδές ΑΒ και ΓΔ ενός κύκλου (Ο, ρ) και ΟΚ, ΟΛ τα αποστήματά τους αντίστοιχα. Τα τρίγωνα ΚΟΑ και ΛΟΓ, έχουν Κ= Λ = 90°, ΟΑ = ΟΓ = ρ και ΑΚ = ΓΛ (αφού ΑΒ = ΓΔ). Επομένως είναι ίσα, οπότε ΟΚ = ΟΛ. Αντίστροφα. Έστω ότι τα αποστήματα ΟΚ και ΟΛ είναι ίσα. Τότε τα τρίγωνα ΚΟΑ και ΛΟΓ έχουν Κ= Λ = 90°, ΟΑ = ΟΓ και ΟΚ = ΟΛ, επομένως είναι ίσα, οπότε:
.
Απάντηση Έστω μια γωνία xÔy και Μ ένα σημείο της διχοτόμου της Οδ . Φέρουμε MA⊥Ox και MB⊥Oy. Τότε τα ορθογώνια τρίγωνα ΑΟΜ και ΒΟΜ είναι ίσα γιατί έχουν Â = B̂ = 90°, ΟΜ κοινή και ΜÔΑ = ΜÔΒ, επομένως ΜΑ = ΜΒ. Αντίστροφα. Έστω Μ ένα εσωτερικό σημείο της γωνίας. Φέρουμε MA⊥Ox και MB⊥Oy και υποθέτουμε ότι ΜΑ = ΜΒ. Τότε τα τρίγωνα ΑΟΜ και ΒΟΜ είναι πάλι ίσα, αφού Â = B̂ = 90°, ΟΜ κοινή και ΜΑ = ΜΒ και επομένως ΜÔΑ = ΜÔΒ, οπότε το Μ είναι σημείο της διχοτόμου Οδ.

Απάντηση Ο κύκλος είναι ένας γεωμετρικός τόπος, αφού όλα τα σημεία του και μόνον αυτά έχουν την ιδιότητα να απέχουν μια ορισμένη απόσταση από ένα σταθερό σημείο. Η μεσοκάθετος ενός τμήματος είναι επίσης ένας γεωμετρικός τόπος, αφού όλα τα σημεία της και μόνον αυτά έχουν την ιδιότητα να ισαπέχουν από τα άκρα του τμήματος. Η διχοτόμος μιας γωνίας είναι ένας άλλος γεωμετρικός τόπος, αφού όλα τα σημεία της και μόνον αυτά (από τα σημεία της γωνίας) ισαπέχουν από τις πλευρές της γωνίας . ΣΧΟΛΙΟ Γεωμετρικός τόπος λέγεται το σύνολο όλων των σημείων, που έχουν μια (κοινή) χαρακτηριστική ιδιότητα.
Απάντηση Δύο σχήματα Σ, Σʹ λέγονται συμμετρικά ως προς ένα σημείο Ο , αν και μόνο αν κάθε σημείο του Σʹ είναι συμμετρικό ενός σημείου του Σ ως προς το Ο και αντίστροφα. ΣΧΟΛΙΟ Το σημείο Ο λέγεται κέντρο συμμετρίας του σχήματος, που αποτελείται από τα συμμετρικά ως προς το Ο σχήματα Σ και Σʹ. Δηλαδή ένα σημείο Ο λέγεται κέντρο συμμετρίας ενός σχήματος, όταν για κάθε σημείο Α του σχήματος το συμμετρικό του Αʹ, ως προς το Ο, είναι επίσης σημείο του σχήματος. Ένα σχήμα με κέντρο συμμετρίας λέμε ότι παρουσιάζει κεντρική συμμετρία. Το ευθύγραμμο τμήμα έχει κέντρο συμμετρίας το μέσο του . Η ευθεία έχει κέντρο συμμετρίας οποιοδήποτε σημείο της . Ο κύκλος έχει κέντρο συμμετρίας το κέντρο του .
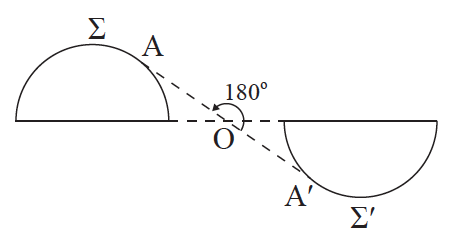
24.Πότε δύο σχήματα Σ, Σʹ λέγονται συμμετρικά ως προς μια ευθεία ε; Απάντηση Δύο σχήματα Σ, Σʹ λέγονται συμμετρικά ως προς την ευθεία ε, αν και μόνον αν κάθε σημείο του Σʹ είναι συμμετρικό ενός σημείου του Σ ως προς την ε και αντίστροφα. ΣΧΟΛΙΟ Η ευθεία ε λέγεται άξονας συμμετρίας του σχήματος που αποτελείται από τα σχήματα Σ και Σʹ. Δηλαδή μια ευθεία ε λέγεται άξονας συμμετρίας ενός σχήματος, όταν για κάθε σημείο Α του σχήματος το συμμετρικό του Αʹ, ως προς την ε, είναι επίσης σημείο του σχήματος. Ένα σχήμα με άξονα συμμετρίας λέμε ότι παρουσιάζει αξονική συμμετρία. Αν ένα σχήμα έχει ως άξονα συμμετρίας μια ευθεία ε, τότε η ε χωρίζει το σχήμα σε δύο μέρη με τέτοιο τρόπο, ώστε, αν διπλώσουμε το φύλλο σχεδίασης κατά μήκος της ε, τα μέρη αυτά θα ταυτιστούν. Η ευθεία έχει άξονα συμμετρίας κάθε ευθεία κάθετη σ’αυτή και τον εαυτό της . Ο κύκλος έχει άξονα συμμετρίας το φορέα κάθε διαμέτρου του . Το ισοσκελές τρίγωνο ΑΒΓ (ΑΒ = ΑΓ) έχει άξονα συμμετρίας το φορέα του ύψους ΑΔ . Το ισόπλευρο τρίγωνο έχει άξονα συμμετρίας τους φορείς των τριών υψών του .

Το ευθύγραμμο τμήμα έχει άξονες συμμετρίας τη μεσοκάθετό του και τον φορέα του .
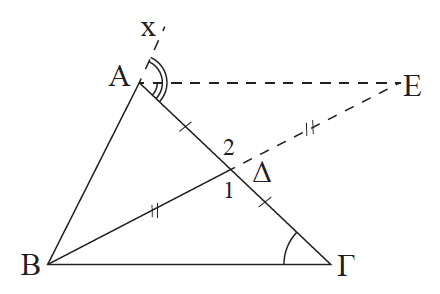
25.Να αποδείξετε ότι κάθε εξωτερική γωνία ενός τριγώνου είναι μεγαλύτερη από καθεμία από τις απέναντι γωνίες του τριγώνου. Απάντηση Έστω τρίγωνο ΑΒΓ. Φέρουμε τη διάμεσο ΒΔ και στην προέκτασή της, προς το Δ, θεωρούμε σημείο Ε, ώστε ΔΕ = ΒΔ. Επειδή το Ε βρίσκεται στο εσωτερικό της γωνίας ΓÂx έχουμε ΓÂΕ < ΓÂx = Âεξ. Όμως τα τρίγωνα ΒΔΓ και ΕΔΑ είναι ίσα γιατί έχουν: ΒΔ = ΔΕ, ΑΔ = ΔΓ και Δ̂1 = Δ̂2, οπότε Γ̂ = ΓÂΕ. Από την τελευταία ισότητα και την ΓÂΕ < Âεξ προκύπτει ότι Âεξ > Γ̂ . Όμοια αποδεικνύεται ότι και Âεξ > B̂. ΣΧΟΛΙΟ Κάθε τρίγωνο έχει το πολύ μια γωνία ορθή ή αμβλεία. Το άθροισμα δύο γωνιών κάθε τριγώνου είναι μικρότερο των 180°.
Απάντηση Έστω τρίγωνο ΑΒΓ με β > γ . Τότε υπάρχει μοναδικό εσωτερικό σημείο Δ της ΑΓ, ώστε ΑΔ = ΑΒ. Το τρίγωνο ΑΒΔ είναι ισοσκελές με βάση ΒΔ και επομένως B̂1 = Δ̂ 1 = ω. Επειδή η ΒΔ είναι εσωτερική ημιευθεία της γωνίας B̂, είναι B̂ > B̂1, ενώ η Δ̂ 1, ως εξωτερική γωνία του τριγώνου ΒΔΓ είναι μεγαλύτερη από τη Γ̂ , δηλαδή Δ̂ 1 > Γ̂ . Έτσι έχουμε B̂ > ω και ω > Γ̂ , επομένως B̂ > Γ̂ . Αντίστροφα. Έστω τρίγωνο ΑΒΓ με B̂ > Γ̂ . Τότε θα είναι και β > γ, γιατί αν ήταν β = γ ή β < γ θα είχαμε B̂ = Γ̂ ή B̂ < Γ̂ αντίστοιχα, που είναι άτοπο. ΣΧΟΛΙO Αν μια γωνία ενός τριγώνου είναι ορθή ή αμβλεία, τότε η απέναντι πλευρά της είναι η μεγαλύτερη πλευρά του τριγώνου. Αν ένα τρίγωνο έχει δύο γωνίες ίσες, τότε είναι ισοσκελές. Αν ένα τρίγωνο έχει και τις τρεις γωνίες του ίσες, τότε είναι ισόπλευρο.

Απάντηση Έστω τρίγωνο ΑΒΓ. Θα αποδείξουμε αρχικά ότι α < β + γ . Γι’ αυτό προεκτείνουμε την πλευρά ΒΑ, προς το Α, κατά τμήμα ΑΔ = ΑΓ. Τότε το τρίγωνο ΑΓΔ είναι ισοσκελές και η ΓΑ εσωτερική ημιευθεία της ΒΓ̂ Δ, οπότε έχουμε αντίστοιχα Δ̂ = Γ̂ 1 και Γ̂ 1 < ΒΓ̂ Δ. Από τις σχέσεις αυτές προκύπτει ότι Δ̂ < ΒΓ̂ Δ, από την οποία σύμφωνα με το προηγούμενο θεώρημα συμπεραίνουμε ότι ΒΓ < ΒΔ ή α < β + γ. Όμοια προκύπτει ότι β < γ + α και γ < α + β. Από τις ανισότητες αυτές, αντίστοιχα προκύπτει ότι α > β – γ, αν β ≥ γ ή α > γ – β, αν γ ≥ β, δηλαδή και στις δύο περιπτώσεις ισχύει το ζητούμενο. Επομένως: β – γ < α < β + γ, β ≥ γ ΣΧΟΛΙΟ Κάθε χορδή κύκλου είναι μικρότερη ή ίση της διαμέτρου.
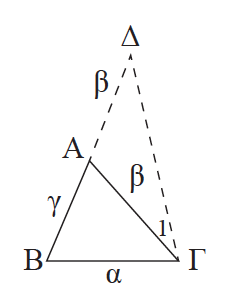
Απάντηση Έστω ΑΒ και ΑΓ δύο ίσα πλάγια τμήματα και ΑΚ το κάθετο τμήμα . To τρίγωνο ΑΒΓ είναι ισοσκελές και το ΑΚ ύψος του, επομένως θα είναι και διάμεσος, δηλαδή ΚΒ = ΚΓ. Αντίστροφα. Έστω ότι ΚΒ = ΚΓ. Στο τρίγωνο ΑΒΓ το ΑΚ είναι ύψος και διάμεσος, άρα το τρίγωνο είναι ισοσκελές, δηλαδή ΑΒ = ΑΓ.
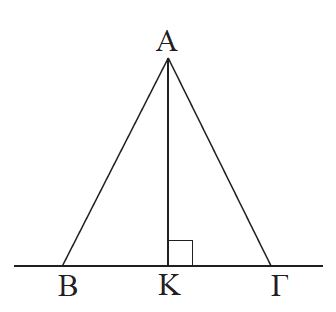
Απάντηση Στο ορθογώνιο τρίγωνο ΑΚΒ , η γωνία K είναι η μεγαλύτερη ως ορθή. Επομένως η πλευρά ΑΒ είναι η μεγαλύτερη πλευρά του τριγώνου και, άρα, ΑΒ > ΑΚ.
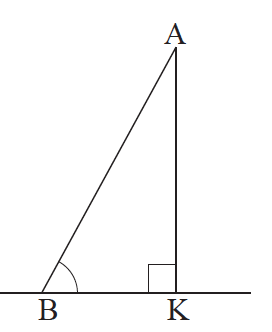
Απάντηση Έστω ευθεία ε και σημείο Α εκτός αυτής. Θεωρούμε την κάθετο ΑΚ στην ε και δύο πλάγια τμήματα ΑΒ, ΑΓ, όπου Β, Γ σημεία της ε .Χωρίς βλάβη της γενικότητας, μπορούμε να υποθέσουμε ότι και τα δύο ίχνη Β, Γ των πλάγιων τμημάτων ανήκουν στην ίδια ημιευθεία που ορίζει το σημείο Κ. Ας υποθέσουμε ότι ΚΓ > ΚΒ . Θα αποδείξουμε ότι ΑΓ > ΑΒ. Αφού το Β είναι μεταξύ των Κ, Γ, η ΑB̂Γ είναι εξωτερική του ορθογώνιου τριγώνου ΚΑΒ, επομένως ΑB̂Γ > K = 90°, δηλαδή η ΑB̂Γ είναι αμβλεία. Στο τρίγωνο ΑΒΓ η πλευρά ΑΓ βρίσκεται απέναντι από την ΑB̂Γ, συνεπώς είναι η μεγαλύτερη πλευρά του τριγώνου, δηλαδή ΑΓ > ΑΒ. Αντίστροφα. Ας υποθέσουμε ότι ΑΓ > ΑΒ. Αν ήταν ΚΓ = ΚΒ, τότε θα είχαμε ΑΓ = ΑΒ, που είναι άτοπο. Αν ΚΓ < ΚΒ, τότε σύμφωνα με το προηγούμενο θα είχαμε ότι ΑΓ < ΑΒ, που είναι επίσης άτοπο. Επομένως ΚΓ > ΚΒ.

Απάντηση Έστω δ > R . Τότε το Α είναι εξωτερικό σημείο του κύκλου, οπότε και κάθε άλλο σημείο Μ της ευθείας είναι εξωτερικό, αφού OM > OA > R. Επομένως, η xʹx δεν έχει κανένα κοινό σημείο με τον κύκλο και λέγεται εξωτερική ευθεία του κύκλου.

Απάντηση Έστω δ = R . Τότε το Α είναι κοινό σημείο της ευθείας με τον κύκλο, ενώ κάθε άλλο σημείο Μ της xʹx είναι εξωτερικό σημείο του (Ο, R), αφού ΟΜ > ΟΑ = R. Επομένως, η xʹx έχει ένα μόνο κοινό σημείο με τον κύκλο και λέγεται εφαπτομένη του κύκλου στο σημείο Α. Το σημείο Α λέγεται σημείο επαφής της ευθείας με τον κύκλο. Επίσης, στην περίπτωση αυτή λέμε ότι η ευθεία xʹx εφάπτεται του κύκλου (Ο, R) στο σημείο Α. Είναι φανερό ότι: Η ακτίνα που καταλήγει στο σημείο επαφής είναι κάθετη στην εφαπτομένη. Η εφαπτομένη του κύκλου σε κάθε σημείο του είναι μοναδική.
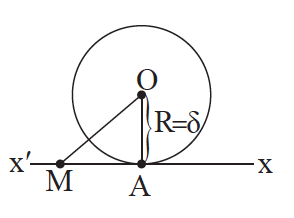
Απάντηση Έστω δ < R . Τότε το Α είναι εσωτερικό σημείο του κύκλου. Πάνω στην ημιευθεία Αx θεωρούμε ένα σημείο Μ, ώστε ΑΜ = R. Τότε το Μ είναι εξωτερικό σημείο του κύκλου, αφού ΟΜ > ΑΜ = R. Έτσι η ημιευθεία Αx, αφού διέρχεται από ένα εσωτερικό σημείο, το Α, και ένα εξωτερικό, το Μ, είναι φανερό ότι έχει ένα μοναδικό κοινό σημείο με τον κύκλο, το Β. Όμοια και η ημιευθεία Αxʹ έχει ένα κοινό σημείο με τον κύκλο, το Βʹ. Επομένως, η xʹx έχει δύο κοινά σημεία με τον κύκλο. Στην περίπτωση αυτή η ευθεία xʹx, λέγεται τέμνουσα του κύκλου και τα κοινά της σημεία με τον κύκλο λέγονται σημεία τομής της με τον κύκλο. Επίσης λέμε ότι η ευθεία τέμνει τον κύκλο. ΓΕΝΙΚΑ Αν δ > R, η ευθεία δεν έχει κοινά σημεία με τον κύκλο. Αν δ = R, η ευθεία έχει ένα μόνο κοινό σημείο με τον κύκλο. Αν δ < R, η ευθεία έχει δύο κοινά σημεία με τον κύκλο.

34.Να αποδείξετε ότι μια ευθεία και ένας κύκλος έχουν το πολύ δύο κοινά σημεία. Απάντηση Ας υποθέσουμε ότι μια ευθεία ε και ένας κύκλος (Ο, ρ) έχουν τρία κοινά σημεία, τα Α, Β, Γ . Επειδή ΟΑ = ΟΒ = ρ και ΟΒ = ΟΓ = ρ, οι μεσοκάθετοι ξ, ζ των ΑΒ, ΒΓ αντίστοιχα, διέρχονται από το Ο. Έτσι από το σημείο Ο έχουμε δύο διαφορετικές κάθετες στην ε, τις ξ, ζ, που είναι άτοπο.
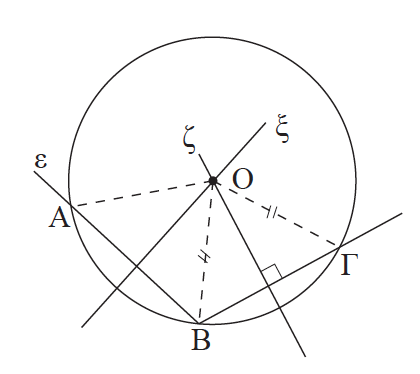
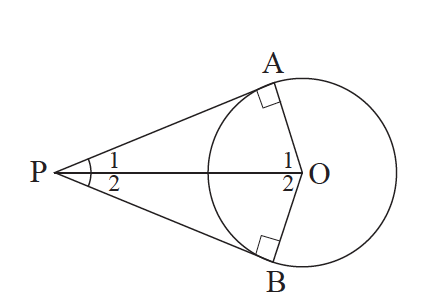
Απάντηση Τα τρίγωνα ΑΟΡ και ΒΟΡ έχουν Â= B̂ = 90°, ΟΡ κοινή και ΟΑ = ΟΒ = ρ , άρα είναι ίσα, οπότε ΡΑ = ΡΒ. ΣΧΟΛΙΟ Αν Ρ είναι ένα εξωτερικό σημείο ενός κύκλου, τότε η διακεντρική ευθεία του: είναι μεσοκάθετος της χορδής του κύκλου με άκρα τα σημεία επαφής, διχοτομεί τη γωνία των εφαπτόμενων τμημάτων και τη γωνία των ακτίνων που καταλήγουν στα σημεία επαφής.
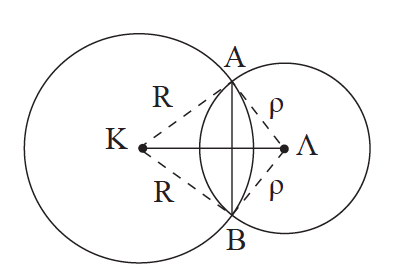
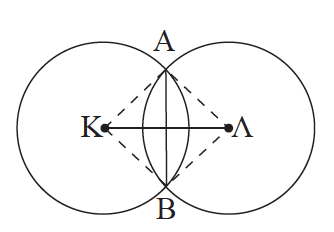
Απάντηση Κύκλοι χωρίς κοινά σημεία Ο κύκλος (Λ, ρ) βρίσκεται στο εσωτερικό του (Κ, R), αν και μόνο αν δ < R – ρ . Οι κύκλοι (Κ, R) και (Λ, ρ) βρίσκεται ο ένας στο εξωτερικό του άλλου, αν και μόνο αν δ > R + ρ . Εφαπτόμενοι κύκλοι Οι κύκλοι εφάπτονται εσωτερικά, δηλαδή έχουν ένα κοινό σημείο και ο κύκλος (Λ, ρ) βρίσκεται στο εσωτερικό του (Κ, R), αν και μόνο αν δ = R – ρ . Οι κύκλοι εφάπτονται εξωτερικά, δηλαδή έχουν ένα κοινό σημείο και ο ένας βρίσκεται στο εξωτερικό του άλλου, αν και μόνο αν δ = R + ρ . (Το κοινό σημείο δύο εφαπτόμενων κύκλων λέγεται σημείο επαφής και είναι σημείο της διακέντρου.) Τεμνόμενοι κύκλοι Οι κύκλοι τέμνονται, δηλαδή έχουν δύο κοινά σημεία, αν και μόνο αν R – ρ < δ < R + ρ . Το ευθύγραμμο τμήμα ΑΒ που ενώνει τα κοινά σημεία λέγεται κοινή χορδή των δύο κύκλων.

Απάντηση Έστω οι κύκλοι (K, R) και (Λ, ρ) και Α, Β τα σημεία τομής τους. Επειδή ΚΑ = ΚΒ = R, το σημείο Κ είναι σημείο της μεσοκαθέτου του ΑΒ. Όμοια από την ΛΑ = ΛΒ = ρ προκύπτει ότι και το Λ είναι σημείο της μεσοκαθέτου του ΑΒ. Άρα, η ΚΛ είναι μεσοκάθετος της κοινής χορδής ΑΒ του κύκλου. ΣΧΟΛΙΟ Στην περίπτωση που οι τεμνόμενοι κύκλοι (Κ, R) και (Λ, ρ) είναι ίσοι, δηλαδή έχουν R = ρ, τότε και η κοινή χορδή είναι μεσοκάθετος της διακέντρου.