Παράλληλες Ευθείες
1.Να αναφέρετε τις σχετικές θέσεις δυο ευθειών οι οποίες βρίσκονται στο ίδιο επίπεδο. Απάντηση Οι σχετικές θέσεις δυο ευθειών ε1 και ε2, οι οποίες βρίσκονται στο ίδιο επίπεδο, είναι οι παρακάτω: Δυο ευθείες ε1 και ε2 που βρίσκονται στο ίδιο επίπεδο και δεν έχουν κοινό σημείο λέγονται παράλληλες ευθείες.
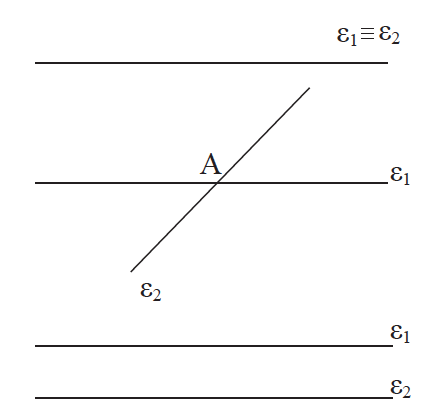
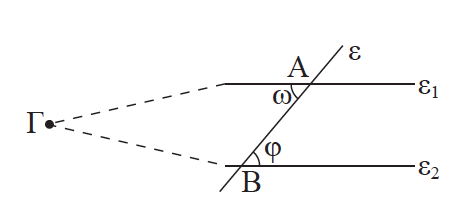
2.Να αποδείξετε οτι αν δύο ευθείες τεμνόμενες από τρίτη σχηματίζουν δύο εντός εναλλάξ γωνίες ίσες, τότε είναι παράλληλες. Απάντηση Έστω ότι ω = φ. Αν οι ευθείες ε1, ε2 τέμνονται σε σημείο Γ, η εξωτερική γωνία φ του τριγώνου ΑΒΓ θα είναι ίση με την απέναντι εσωτερική γωνία ω, που είναι άτοπο. Άρα ε1 // ε2. ΠΟΡΙΣΜΑ Αν δύο ευθείες τεμνόμενες από τρίτη σχηματίζουν δύο εντός, εκτός και επί τα αυτά μέρη γωνίες ίσες ή δύο εντός και επί τα αυτά μέρη παραπληρωματικές, τότε είναι παράλληλες.
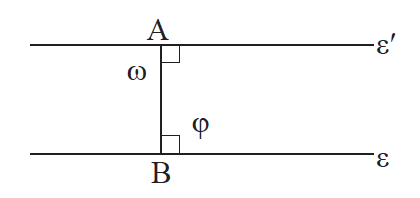
3.Δύο ευθείες κάθετες στην ίδια ευθεία, σε διαφορετικά σημεία της, είναι μεταξύ τους παράλληλες. Απάντηση Πράγματι οι γωνίες ω και φ είναι ορθές, οπότε ω = φ. Άρα ε // ε΄. Θα εξετάσουμε τώρα αν από σημείο εκτός ευθείας μπορούμε να φέρουμε παράλληλες ευθείες προς αυτή και πόσες. Έστω λοιπόν, ευθεία ε και σημείο Α εκτός αυτής. Φέρουμε την ΑΒ⊥ε και ονομάζουμε εʹ την ευθεία που είναι κάθετη στην ΑΒ στο σημείο Α. Τότε εʹ//ε (αφού και οι δύο είναι κάθετες στην ΑΒ). Αίτημα παραλληλίας
Από σημείο εκτός ευθείας άγεται μία μόνο παράλληλη προς αυτή.
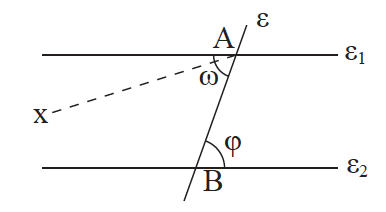
4.Να αποδείξετε οτι αν δυο παράλληλες ευθείες τέμνονται από τρίτη, σχηματίζουν τις εντός εναλλάξ γωνίες ίσες. Απάντηση Έστω ότι ε1 // ε2 και ε μια τέμνουσα . Θα αποδείξουμε π.χ. ότι ω = φ. Αν οι γωνίες ω και φ δεν είναι ίσες, φέρουμε την Αx ώστε οι γωνίες xÂB και φ να βρίσκονται εκατέρωθεν της ε και να είναι ίσες. Τότε Αx // ε2 γιατί τεμνόμενες από την ΑΒ σχηματίζουν δύο εντός και εναλλάξ γωνίες ίσες. Κατά συνέπεια υπάρχουν δύο παράλληλες από το Α προς την ε2, που είναι άτοπο. Άρα ω = φ. ΠΟΡΙΣΜΑ Αν δύο παράλληλες ευθείες τέμνονται από τρίτη σχηματίζουν τις εντός και επί τα αυτά μέρη γωνίες παραπληρωματικές.
Αν δύο παράλληλες ευθείες τέμνονται από τρίτη σχηματίζουν τις εντός εκτός και επί τα αυτά μέρη γωνίες ίσες.
Απάντηση Αν οι ε1 και ε2 τέμνονταν σε σημείο Α, θα είχαμε από το Α δύο παράλληλες προς την ε, που είναι άτοπο. Άρα ε1//ε2.
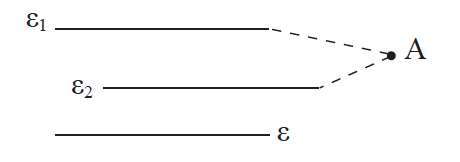
Απάντηση Υποθέτουμε ότι η ε τέμνει την ε1 στο Α. Αν η ε δεν έτεμνε την ε2, θα ήταν ε//ε2 και έτσι θα είχαμε από το Α δύο παράλληλες προς την ε2, πράγμα αδύνατο. Άρα η ε τέμνει την ε2. ΠΟΡΙΣΜΑ
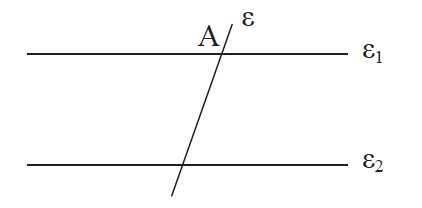
Αν μια ευθεία είναι κάθετη σε μια από δύο παράλληλες ευθείες, τότε είναι κάθετη και στην άλλη.
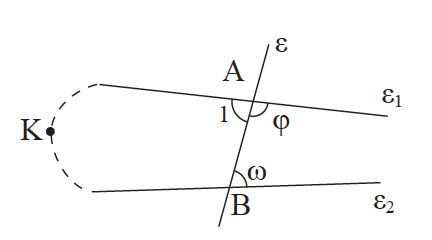
Απάντηση Έστω ότι η ε τέμνει τις ε1, ε2 στα Α και Β αντίστοιχα και ότι φ + ω ≠ 90°. Τότε οι ε1 και ε2 δεν είναι παράλληλες, αφού φ + ω ≠ 90° . Έστω ότι οι ε1 και ε2 τέμνονται σε σημείο Κ, προς το μέρος της τέμνουσας, που δεν περιέχει τις γωνίες ω και φ. Τότε, όμως, η εξωτερική γωνία ω του τριγώνου ΑΚΒ είναι μεγαλύτερη από τη γωνία Â1, δηλαδή ω > Â1 = 90° – φ ή ω + φ > 90°, που είναι άτοπο. Άρα οι ε1, ε2 τέμνονται προς το μέρος της τέμνουσας που βρίσκονται οι γωνίες ω και φ. ΠΟΡΙΣΜΑ Η κατασκευή τριγώνου με δοσμένη μία πλευρά και τις δύο προσκείμενες σε αυτή γωνίες έχει λύση, αν και μόνο αν το άθροισμα των δύο γωνιών είναι μικρότερο των δύο ορθών.
8.Τι σχέση έχουν δυο γωνίες με πλευρές παράλληλες; Απάντηση Δύο γωνίες που έχουν τις πλευρές τους παράλληλες, μία προς μία, είναι ίσες αν είναι και οι δύο οξείες ή αμβλείες, ενώ είναι παραπληρωματικές αν η μία γωνία είναι οξεία και η άλλη αμβλεία.
9.Ποιός κύκλος λέγεται περιγεγραμμένος κύκλος ενός τριγώνου; Απάντηση Περιγεγραμμένος κύκλος ενός τριγώνου λέγεται ο κύκλος που διέρχεται από τις τρεις κορυφές του. Επιπλέον αποδεικνύεται ότι το κέντρο του είναι ένα σημείο στο οποίο συντρέχουν και οι τρεις μεσοκάθετοι του τριγώνου και λέγεται περίκεντρο.
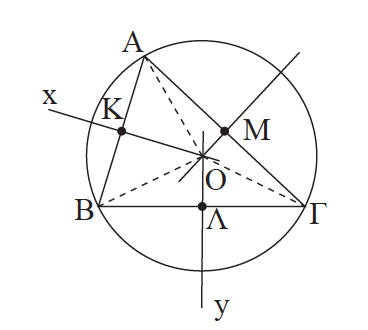
10.Να αποδείξετε οτι οι τρεις μεσοκάθετοι ενός τριγώνου διέρχονται από το ίδιο σημείο, το οποίο είναι κέντρο κύκλου που διέρχεται από τις κορυφές του τριγώνου. Απάντηση Έστω τρίγωνο ΑΒΓ και Κ, Λ, Μ τα μέσα των πλευρών του ΑΒ, ΒΓ και ΑΓ αντίστοιχα. Οι μεσοκάθετοι Κx και Λy των ΑΒ, ΒΓ θα τέμνονται σε σημείο Ο, αφού τέμνονται οι κάθετες ευθείες τους ΑΒ και ΒΓ. Το Ο ισαπέχει από τις κορυφές Α και Β αφού ανήκει στη μεσοκάθετο της πλευράς ΑΒ, δηλαδή ΟΑ = ΟΒ. Επίσης ΟΒ = ΟΓ, αφού το Ο ανήκει στη μεσοκάθετο της πλευράς ΒΓ. Επομένως ισχύει ότι ΟΑ = ΟΓ, οπότε το Ο θα ανήκει και στη μεσοκάθετο της ΑΓ. Άρα, ο κύκλος (O, OA) θα διέρχεται από τις τρεις κορυφές του τριγώνου ΑΒΓ και είναι ο περιγεγραμμένος κύκλος του τριγώνου.
Απάντηση Εγγεγραμμένος κύκλος ενός τριγώνου λέγεται ο κύκλος που βρίσκεται στο εσωτερικό τριγώνου και εφάπτεται και στις τρεις πλευρές του.Επιπλέον αποδεικνύεται ότι το κέντρο του, το οποίο λέγεται έγκεντρο, θα είναι το σημείο τομής των διχοτόμων των γωνιών του τριγώνου.
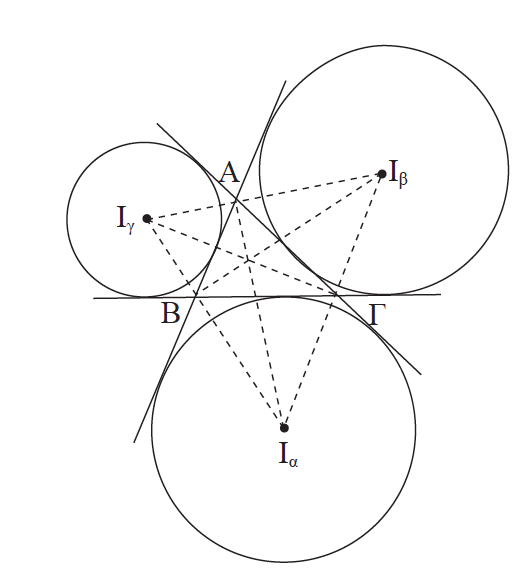
12.Να αποδείξετε οτι οι διχοτόμοι των γωνιών ενός τριγώνου διέρχονται από το ίδιο σημείο, το οποίο είναι κέντρο κύκλου που εφάπτεται και στις τρεις πλευρές του τριγώνου. Απάντηση Έστω τρίγωνο ΑΒΓ και οι διχοτόμοι ΒΕ και ΓΖ των γωνιών του B̂ και Γ̂ αντίστοιχα. Οι ΒΕ και ΓΖ τέμνονται σε σημείο I ,αφού ΣΧΟΛΙΟ Η ιδιότητα των εσωτερικών διχοτόμων ενός τριγώνου να διέρχονται από το ίδιο σημείο ισχύει και όταν θεωρήσουμε δύο εξωτερικές και μία εσωτερική διχοτόμο του τριγώνου. Οι τρεις αυτές διχοτόμοι τέμνονται σε σημείο το οποίο είναι κέντρο κύκλου που εφάπτεται στη μία πλευρά του τριγώνου και στις προεκτάσεις των δύο άλλων. Ο κύκλος αυτός λέγεται παρεγγεγραμμένος και το κέντρο του παράκεντρο του τριγώνου. Σε κάθε τρίγωνο υπάρχουν τρία παράκεντρα, τα οποία συμβολίζουμε Ια, Ιβ, Ιγ, και κατά συνέπεια τρεις παρεγγεγραμμένοι κύκλοι .
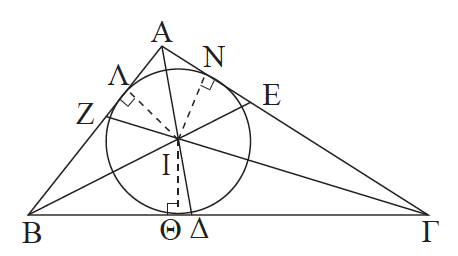
. Το Ι ως σημείο της διχοτόμου της B θα ισαπέχει από τις πλευρές της ΒΑ και ΒΓ, δηλαδή ΙΛ = ΙΘ. Ανάλογα το Ι θα ισαπέχει από τις πλευρές της Γ̂ , δηλαδή ΙΘ = ΙΝ. Επομένως το Ι ισαπέχει από τις ΑΒ και ΑΓ και θα ανήκει στη διχοτόμο της γωνίας Â. Τελικά, το Ι είναι το σημείο τομής και των τριών διχοτόμων του τριγώνου. Με κέντρο το Ι και ακτίνα την κοινή απόσταση του Ι από τις πλευρές του ΑΒΓ, γράφεται κύκλος που εφάπτεται και στις τρεις πλευρές του τριγώνου.
13.Να αποδείξετε οτι το άθροισμα των γωνιών κάθε τριγώνου είναι 2 ορθές. Απάντηση ΠΟΡΙΣΜΑ
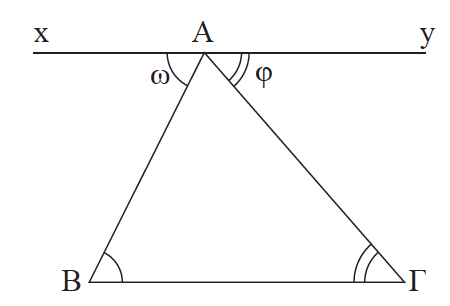
Από μια κορυφή, π.χ. την Α, φέρουμε ευθεία xy//BΓ. Τότε ω = B̂ (1) και φ = Γ̂ (2), ως εντός και εναλλάξ των παραλλήλων xy και ΒΓ με τέμνουσες ΑΒ και ΑΓ αντίστοιχα. Αλλά ω + Â + φ = 180° (3).
Από τις (1), (2) και (3) προκύπτει ότι Â + B̂ + Γ̂ = 180° .
14.Να αποδείξετε οτι κάθε εξωτερική γωνία τριγώνου είναι ίση με το άθροισμα των δύο απέναντι εσωτερικών γωνιών του τριγώνου. Απάντηση Έχουμε Â + B̂ + Γ̂ = 180° και Γ̂ εξ + Γ̂ = 180°, οπότε Â + B̂ + Γ̂ = Γ̂ εξ + Γ̂ ή Γ̂ εξ = Â + B̂ .
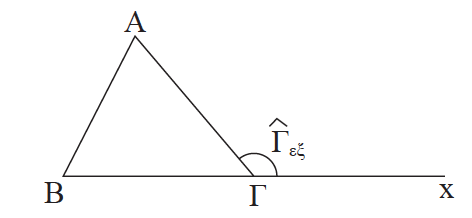
15.Τι σχέση έχουν δυο γωνίες με πλευρές κάθετες; Απάντηση Δύο γωνίες που έχουν τις πλευρές τους κάθετες, μία προς μία, είναι ίσες αν είναι και οι δύο οξείες ή αμβλείες, ενώ είναι παραπληρωματικές αν η μία γωνία είναι οξεία και η άλλη αμβλεία.
Απάντηση Έστω οι γωνίες xÔy = ω και xʹÔʹyʹ= φ με Οx⊥Oʹxʹ και Oy⊥Oʹyʹ.Τα τρίγωνα ΟΑΓ και ΟʹΒΓ έχουν Â = B̂ = 90° και Γ̂ 1 = Γ̂ 2 (κατακορυφήν).
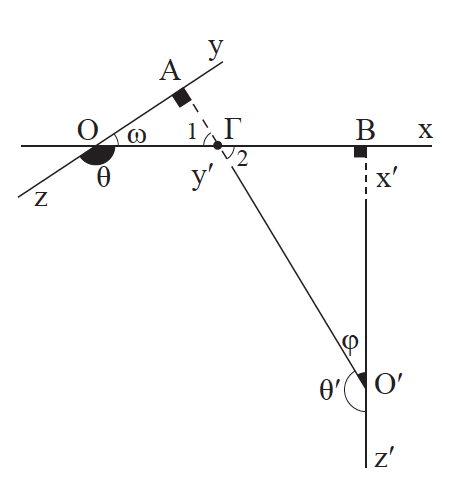
Άρα θα έχουν και τις άλλες γωνίες ίσες, οπότε ω = φ.
Απάντηση Πράγματι, είναι θ + ω = 180°, θʹ + φ = 180°, οπότε θ = θʹ, αφού ω = φ.

Απάντηση Πράγματι, είναι θ + ω = 180°, οπότε θ + φ =180°, αφού ω = φ.

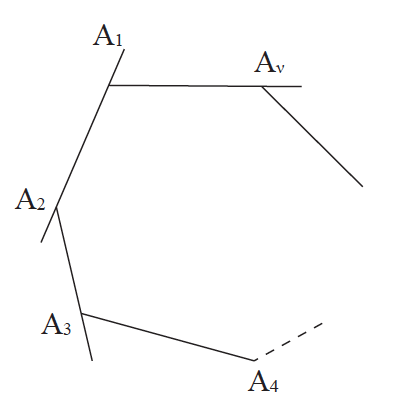
Απάντηση Ας θεωρήσουμε κυρτό πολύγωνο Α1Α2… Αν με ν πλευρές και ας φέρουμε από μια κορυφή του, π.χ. την Α1, όλες τις διαγωνίους που διέρχονται από αυτή. Έτσι το πολύγωνο διαιρείται σε ν – 2 τρίγωνα, γιατί σε καθεμιά από τις πλευρές του, εκτός των Α1Α2 και Α1Αν που διέρχονται από την κορυφή Α1, αντιστοιχεί ένα τρίγωνο. Επειδή το άθροισμα των γωνιών των ν – 2 τριγώνων είναι 2(ν – 2) = (2ν – 4) ορθές και ισούται με το άθροισμα των γωνιών του πολυγώνου, προκύπτει ότι: Το άθροισμα των γωνιών κυρτού ν-γώνου είναι 2ν – 4 ορθές.
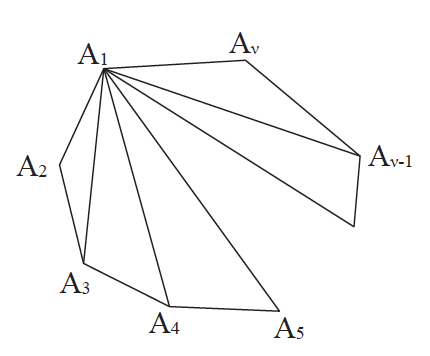
Απάντηση Έχουμε: Â1εξ + Â1 = 180° Â2εξ + Â2 = 180° …….. + …… = … Âνεξ + Âν = 180° Προσθέτουμε κατά μέλη οπότε: · (Â1εξ + Â2εξ + … + Âνεξ) + (Â1 + Â2 + … + Âν) = ν·180° ή (Â1εξ + Â2εξ + … + Âνεξ) + (2ν – 4)·90° = ν·180° ή Â1εξ + Â2εξ+ … + Âνεξ = 360°.