Εμβαδά
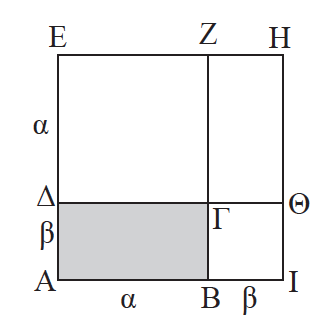
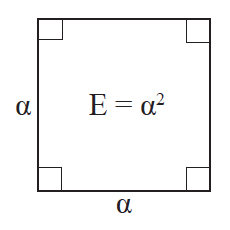
1.Να αποδείξετε οτι το εμβαδόν ενός ορθογωνίου ισούται με το γινόμενο των πλευρών του. Απάντηση Έστω ένα ορθογώνιο ΑΒΓΔ, με ΑΒ = α και ΑΔ = β .Θα αποδείξουμε οτι το εμβαδόν του ορθογωνίου είναι: Ε = α ∙ β . Προεκτείνουμε την πλευρά ΑΔ κατά τμήμα ΔΕ = α, την ΑΒ κατά ΒΙ = β και σχηματίζουμε το τετράγωνο ΑΙΗΕ, το οποίο είναι φανερό ότι έχει πλευρά α + β και επομένως είναι: (ΑΙΗΕ) = (α + β) 2 (1). Προεκτείνοντας τις ΔΓ και ΒΓ σχηματίζονται τα τετράγωνα ΔΓΖΕ, ΒΙΘΓ με πλευρές α, β αντίστοιχα και το ορθογώνιο ΓΘΗΖ που είναι ίσο με το ΑΒΓΔ. Έτσι έχουμε (ΔΓΖΕ) = α 2, (ΒΙΘΓ) = β 2 και (ΓΘΗΖ) = (ΑΒΓΔ) (2) . Είναι φανερό όμως ότι (ΑΙΗΕ) = (ΑΒΓΔ) + (ΓΘΗΖ) + (ΒΙΘΓ) + (ΔΓΖΕ), από την οποία με τη βοήθεια των (1) και (2) προκύπτει ότι: (α + β) 2 = 2(ΑΒΓΔ) + α 2 + β 2. Από αυτή μετά τις πράξεις καταλήγουμε στη σχέση (ΑΒΓΔ) = α ∙ β. ΣΧΟΛΙΟ Το εμβαδόν Ε ενός τετραγώνου πλευράς α είναι α 2, δηλαδή: Ε = α 2. Για το εμβαδόν δεχόμαστε ότι ισχύουν οι επόμενες ιδιότητες (αξιώματα):
Απάντηση Έστω ένα παραλληλόγραμμο ΑΒΓΔ, με ΑΒ = β και ΒΓ = α και υα, υβ τα αντίστοιχα ύψη. Θα αποδείξουμε οτι το εμβαδόν του παραλληλογράμμου είναι: Ε = α·υα = β·υβ . Φέρνουμε το ύψος ΑΖ που αντιστοιχεί στη ΒΓ. Από το Δ φέρουμε ΔΗ κάθετη στην προέκταση της ΒΓ. Τότε τα τρίγωνα ΖΒΑ και ΗΓΔ είναι ίσα (Ẑ = Ĥ = 90°, ΑΒ = ΔΓ και B̂ 1 = Γ̂ 1), οπότε: (ΖΒΑ) = (ΗΓΔ) (1). Από το σχήμα όμως έχουμε ότι (ΑΒΓΔ) = (ABZ) + (ΑΖΓΔ), οπότε σύμφωνα με την (1) προκύπτει ότι (ΑΒΓΔ) = (ΑΖΓΔ) + (ΔΓΗ) = (ΑΖΗΔ). Επομένως σύμφωνα με το προηγούμενο θεώρημα έχουμε (ΑΒΓΔ) = (ΑΖΗΔ) = ΑΔ ∙ ΑΖ = ΒΓ ∙ ΑΖ,που είναι το ζητούμενο. ΣΧΟΛΙΟ Το εμβαδόν του ρόμβου ,αλλά και οποιουδήποτε κυρτού ή μη κυρτού, τετραπλεύρου με κάθετες διαγωνίους ισούται με το ημιγινόμενο των διαγωνίων του.
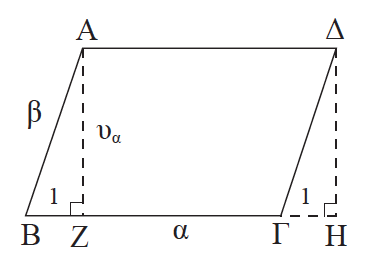
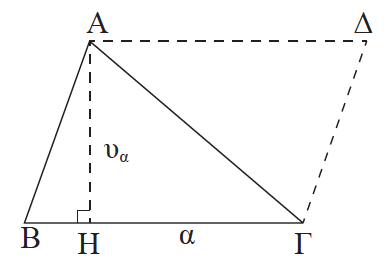
Απάντηση Έστω ΑΒΓ τρίγωνο ,θα αποδείξουμε οτι Με πλευρές ΑΒ και ΒΓ σχηματίζουμε το παραλληλόγραμμο ΑΒΓΔ, το εμβαδόν του οποίου είναι (ΑΒΓΔ) = α∙υα (1). ΣΧΟΛΙΟ Το εμβαδόν Ε ενός ισόπλευρου τριγώνου πλευράς α είναι ίσο με Το εμβαδόν Ε ενός ορθογωνίου τριγώνου με κάθετες πλευρές β και γ είναι ίσο με Η διάμεσος ενός τριγώνου διχοτομεί το εμβαδόν του.
.
Όμως τα τρίγωνα ΑΒΓ και ΔΑΓ είναι ίσα, οπότε: (ΑΒΓ) = (ΑΔΓ) (2).
Από το σχήμα έχουμε ότι (ΑΒΓΔ) = (ΑΒΓ) + (ΑΓΔ) η οποία, σύμφωνα με τις (1) και (2), μετατρέπεται στην α · υα = 2(ΑΒΓ) ή .
.
.
Απάντηση Έστω τραπέζιο ΑΒΓΔ (ΒΓ//ΑΔ) με βάσεις ΒΓ = Β, ΑΔ = β και υ το ύψος του. Θα αποδείξουμε οτι Φέρουμε τη διαγώνιο ΑΓ. Τότε έχουμε Ε = (ΑΒΓΔ) = (ΑΒΓ) + (ΑΓΔ) (1). Με αντικατάσταση των σχέσεων (2) στην (1) προκύπτει ότι ΠΟΡΙΣΜΑ Το εμβαδόν τραπεζίου ισούται με το γινόμενο της διαμέσου επί το ύψος του.
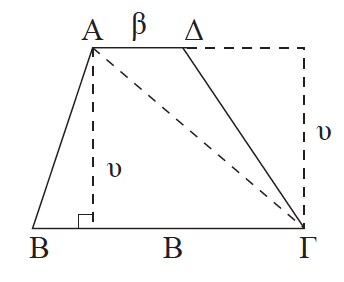
.
Αλλά τα δύο τρίγωνα ΑΒΓ και ΑΓΔ έχουν το ίδιο ύψος υ και βάσεις Β, β αντίστοιχα και επομένως: και
(2)
, δηλαδή το ζητούμενο.
Απάντηση Γνωρίζουμε απο προηγούμενη εφαρμογή οτι Επομένως (τύπος του Ήρωνα), όπου τ η ημιπερίμετρος του τριγώνου.
, οπότε έχουμε:
.
.
Απάντηση Έστω τρίγωνο ΑΒΓ και ο εγγεγραμμένος κύκλος του (Ι, ρ). Φέρουμε τα τμήματα ΙΑ, ΙΒ και ΙΓ και έτσι το τρίγωνο χωρίζεται στα τρίγωνα ΙΒΓ, ΙΓΑ και ΙΑΒ που έχουν το ίδιο ύψος ρ και δεν έχουν κοινά εσωτερικά σημεία, οπότε έχουμε: Ε = (ΑΒΓ) = (ΙΒΓ) + (ΙΓΑ) + (ΙΑΒ) =
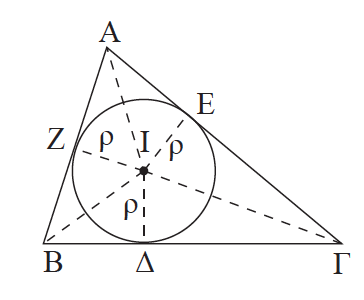
.
Απάντηση Είναι γνωστό ότι βγ = 2Rυα , οπότε έχουμε ότι , όπου R η ακτίνα του περιγεγραμμένου κύκλου του τριγώνου.
και με αντικατάσταση στον τύπο
προκύπτει το ζητούμενο.
Απάντηση Αν  < 90° , από το ορθογώνιο τρίγωνο ΔΒΑ προκύπτει ότι: υβ = γ∙ημÂ. Αν  > 90°, πάλι από το ορθογώνιο τρίγωνο ΔΒΑ προκύπτει ότι: υβ = γ ∙ ημÂεξ = γ ∙ ημ(180ο – Â)= γ ∙ ημÂ. Έτσι και στις δύο περιπτώσεις έχουμε υβ = γ ∙ ημ οπότε: Όταν  =90°, τότε υβ = γ, επομένως πάλι ο τύπος ισχύει. Όμοια αποδεικνύονται και οι υπόλοιποι τύποι. ΣΧΟΛΙΟ Νόμος ημιτόνων Σε κάθε τρίγωνο ΑΒΓ ισχύει ότι: .
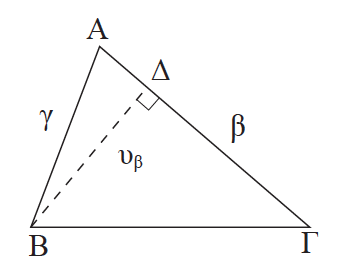
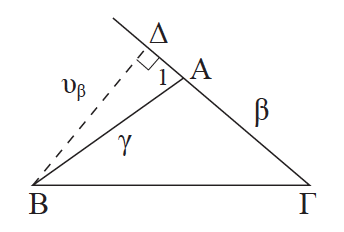
.
.
9.Mε πόσο ισούται ο λόγος των εμβαδών δυο τριγώνων ,αν αυτά έχουν ίσες βάσεις; Απάντηση Αν δύο τρίγωνα έχουν ίσες βάσεις, τότε ο λόγος των εμβαδών τους ισούται με το λόγο των αντίστοιχων υψών.
Απάντηση Αν δύο τρίγωνα έχουν ίσα ύψη, τότε ο λόγος των εμβαδών τους ισούται με το λόγο των αντίστοιχων βάσεων.
Απάντηση Έστω δύο όμοια τρίγωνα ΑΒΓ και ΑʹΒʹΓʹ με Â= Âʹ και B̂ = B̂ ʹ. Τότε Από τις (1) και (2) προκύπτει ότι ΣΧΟΛΙΟ Το παραπάνω συμπέρασμα ισχύει γενικότερα και για όμοια πολύγωνα, όπως μας βεβαιώνει το επόμενο θεώρημα: Ο λόγος των εμβαδών δύο όμοιων πολυγώνων είναι ίσος με το τετράγωνο του λόγου ομοιότητάς τους.
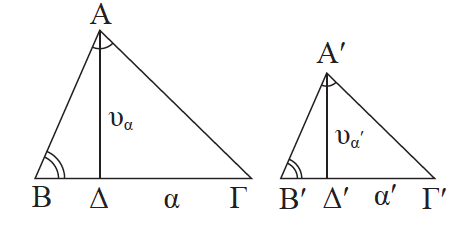
(1), όπου λ ο λόγος ομοιότητας. Αλλά όπως και παραπάνω, είναι
(2).
.
Απάντηση Θεωρούμε τα τρίγωνα ΑΒΓ και ΑʹΒʹΓʹ με  = Âʹ ή Â + Âʹ = 180° . Τότε και στις δύο περιπτώσεις θα ισχύει ημ = ημÂʹ, οπότε από τις ισότητες
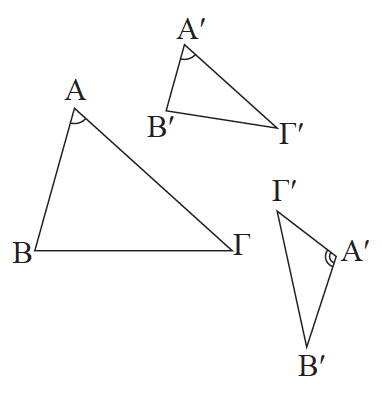
και
με διαίρεση κατά μέλη προκύπτει ότι
, που είναι το ζητούμενο.
