Για να ξεκινήσετε πατήστε ΕΚΚΙΝΗΣΗ ΚΟΥΙΖ
Περίληψη κουίζ
Ολοκληρώθηκαν 0 από 10 ερωτήσεις
Ερωτήσεις:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
Πληροφορίες
Διαγώνισμα 4 – Όρια & Συνέχεια
Έχεις ήδη ολοκληρώσει το κουίζ. Δεν μπορείς, λοιπόν, να το ξεκινήσεις ξανά.
Το κουίζ φορτώνεται...
Πρέπει να συνδεθείτε ή να εγγραφείτε για να ξεκινήσετε το κουίζ.
Πρέπει να ολοκληρώσεις το επόμενο κουίζ για να ξεκινήσεις αυτό το κουίζ:
Αποτελέσματα
Απαντήθηκαν σωστά 0 από 10 ερωτήσεις
Ο χρόνος σου:
Ό χρόνος πέρασε
Έφτασες 0 από 0 βαθμούς, (0)
Κατηγορίες
- Χωρίς κατηγορία 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- Απαντήθηκε
- Ανασκόπηση
-
Ερώτηση 1 από 10
1. Ερώτηση
2 βαθμοίΗ συνάρτηση f είναι 1-1, αν και μόνο αν κάθε οριζόντια ευθεία τέμνει τη γραφική παράσταση της f το πολύ σε ένα σημείο.
-
Ερώτηση 2 από 10
2. Ερώτηση
2 βαθμοίΑν
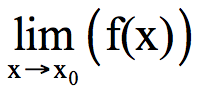 = 0 και f(x) < 0 κοντά στο xo τότε
= 0 και f(x) < 0 κοντά στο xo τότε 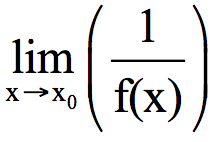 = +∞.
= +∞. -
Ερώτηση 3 από 10
3. Ερώτηση
2 βαθμοίΑν μια συνάρτηση f είναι γνησίως φθίνουσα και συνεχής σε ένα ανοικτό διάστημα (α, β), τότε το σύνολο τιμών της στο διάστημα αυτό είναι το διάστημα (Α,Β), όπου Α =
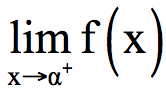 και Β =
και Β = 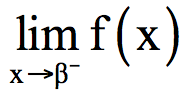 .
. -
Ερώτηση 4 από 10
4. Ερώτηση
2 βαθμοίΑν
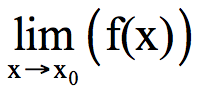 < 0, τότε f(x) < 0 κοντά στο x0 .
< 0, τότε f(x) < 0 κοντά στο x0 . -
Ερώτηση 5 από 10
5. Ερώτηση
2 βαθμοίΑν
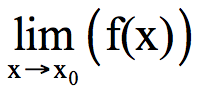 = +∞ ή -∞ ,τότε
= +∞ ή -∞ ,τότε 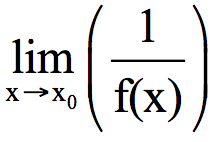 = 0.
= 0. -
Ερώτηση 6 από 10
6. Ερώτηση
2 βαθμοίΜια συνάρτηση f:A → ℝ λέγεται συνάρτηση 1-1, όταν για οποιαδήποτε x1, x2 ∈ A ισχύει η συνεπαγωγή : αν x1≠ x2, τότε f(x1) ≠ f(x2).
-
Ερώτηση 7 από 10
7. Ερώτηση
2 βαθμοίΙσχύει ότι:
 .
. -
Ερώτηση 8 από 10
8. Ερώτηση
2 βαθμοίΜία συνάρτηση f με πεδίο ορισμού Α θα λέμε ότι παρουσιάζει στο x0∈A (ολικό) μέγιστο το f(x0), όταν f(x) ≤ f(x0) για κάθε x∈A.
-
Ερώτηση 9 από 10
9. Ερώτηση
2 βαθμοίΑν μια συνάρτηση f είναι γνησίως μονότονη σε ένα διάστημα Δ, τότε είναι και 1-1 στο διάστημα αυτό.
-
Ερώτηση 10 από 10
10. Ερώτηση
2 βαθμοίΑν είναι
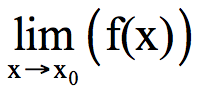 = +∞ , τότε f(x) < 0 κοντά στο x0.
= +∞ , τότε f(x) < 0 κοντά στο x0.
ΚΑΛΗ ΕΠΙΤΥΧΙΑ
