ΑΛΓΕΒΡΙΚΗ ΕΠΙΛΥΣΗ ΓΡΑΜΜΙΚΟΥ ΣΥΣΤΗΜΑΤΟΣ

ΑΛΓΕΒΡΙΚΗ ΕΠΙΛΥΣΗ ΓΡΑΜΜΙΚΟΥ ΣΥΣΤΗΜΑΤΟΣ

Σχολικό βιβλίο (εμπλουτισμένο)

ΑΝΑΛΥΤΙΚΗ ΜΕΘΟΔΟΛΟΓΙΑ

ΜΕΘΟΔΟΣ ΑΝΤΙΚΑΤΑΣΤΑΣΗΣ

Για παράδειγμα θα λύσουμε το σύστημα .

1ο ΒΗΜΑ

Λύνουμε μία από τις εξισώσεις του συστήματος ως προς έναν άγνωστο.

(Όποια θέλουμε…στην ουσία όποια απο τις δύο θεωρούμε ποιό εύκολο να επιλυθεί)

Στο παράδειγμά μας θα επιλέξουμε την εξίσωση $2x+y=0\Leftrightarrow y=-2x$

Επομένως το σύστημά θα πάρει τη μορφή: .

2ο ΒΗΜΑ

Aντικαθιστούμε στην άλλη εξίσωση του συστήματος τον άγνωστο αυτόν με την ίση παράστασή του, οπότε προκύπτει εξίσωση με έναν άγνωστο, την οποία και λύνουμε.

επομένως…

3ο ΒΗΜΑ

Tην τιμή του αγνώστου που βρήκαμε την αντικαθιστούμε στην προηγούμενη εξίσωση, οπότε βρίσκουμε και τον άλλο άγνωστο.

Άρα έχουμε .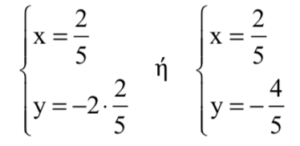

4ο ΒΗΜΑ

Προσδιορίζουμε τη λύση του συστήματος.

Τελικά το Σύστημα έχει μοναδική λύση $(x,y)=(\frac{2}{5},-\frac{4}{5})$

Για επαλήθευση, αντικαθιστούμε τις τιμές $x=\frac{2}{5} ,y=-\frac{4}{5}$ στις εξισώσεις του συστήματος και διαπιστώνουμε ότι το ζεύγος $(\frac{2}{5},-\frac{4}{5})$ είναι λύση του.

Στην ίδια λύση θα καταλήγαμε και αν λύναμε μία από τις εξισώσεις του συστήματος ως προς x.

Γραφική Επίλυση

βιντεοπαρουσίαση – Μέθοδος αντικατάστασης

ΜΕΘΟΔΟΣ ΑΝΤΙΘΕΤΩΝ ΣΥΝΤΕΛΕΣΤΩΝ

Για παράδειγμα θα λύσουμε το σύστημα .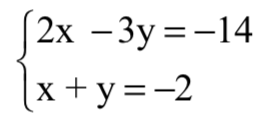

1ο ΒΗΜΑ

Πολλαπλασιάζουμε τα μέλη κάθε εξίσωσης με κατάλληλο αριθμό, ώστε να εμφανιστούν αντίθετοι συντελεστές σ’ έναν από τους δύο αγνώστους προκειμένου να τον απαλείψουμε.

Στο παράδειγμά μας θα πολλαπλασιάσουμε την εξίσωση $x+y=-2$ με τον αριθμό 3 ώστε να προκύψουν αντίθετοι συντελεστές στη μεταβλητή y.

επομένως το σύστημα θα πάρει τη μορφή .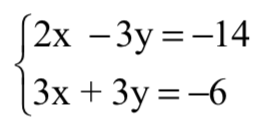

2ο ΒΗΜΑ

Προσθέτουμε κατά μέλη τις δύο εξισώσεις, οπότε προκύπτει εξίσωση με έναν άγνωστο την οποία και λύνουμε.

Προσθέτοντας κατα μέλη τις εξισώσεις του συστήματος και αφού τα μονώνυμα 3y και -3y είναι αντίθετα προκύπτει η εξίσωση $5x=-20$ και το σύστημα έχει πάρει τη μορφή όπου προκύπτει ότι $x=-4$ .

3ο ΒΗΜΑ

Αντικαθιστούμε την τιμή του αγνώστου που βρήκαμε σε μία από τις δύο εξισώσεις του συστήματος, οπότε βρίσκουμε την τιμή και του άλλου αγνώστου.

αντικαθιστώντας όπου $x=-4$ σε όποια από τις δύο εξισώσεις επιθυμώ θα προκύψει ότι $y=2$ δηλαδή .