Απάντηση ΠΡΟΣΟΧΗ Οι πράξεις μεταξύ των ορίων μπορούν να γίνουν μόνο αν το όριο κάθε μιας απο τις συναρτήσεις ,υπάρχει και είναι πραγματικός αριθμός. και
με
πως βρίσκουμε τα όρια στο x0 των συναρτήσεων
;
16.Πότε λέμε ότι μια συνάρτηση f, με πεδίο ορισμού Α, είναι συνεχής; Απάντηση Μια συνάρτηση f με πεδίο ορισμού το Α λέγεται συνεχής αν για κάθε x0∈A ισχύει ΠΑΡΑΤΗΡΗΣΗ Χαρακτηριστικό γνώρισμα μιας συνεχούς συνάρτησης σε ένα κλειστό διάστημα είναι ότι η γραφική της παράσταση είναι μια συνεχής καμπύλη, δηλαδή για το σχεδιασμό της δε χρειάζεται να σηκώσουμε το μολύβι από το χαρτί.Αποδεικνύεται ότι οι γνωστές μας συναρτήσεις, πολυωνυμικές, τριγωνομετρικές, εκθετικές, λογαριθμικές, αλλά και όσες προκύπτουν από πράξεις μεταξύ αυτών είναι συνεχείς συναρτήσεις.
.
17.Πότε μια συνάρτηση f είναι παραγωγίσιμη σε ένα σημείο x0 του πεδίου ορισμού της ; Απάντηση Το όριο αυτό ονομάζεται παράγωγος της f στο x0, συμβολίζεται με f ΄(x0) και διαβάζεται “ f τονούμενο του x0”. Έχουμε λοιπόν:
Μια συνάρτηση f με πεδίο ορισμού είναι παραγωγίσιμη σε ένα σημείο x0 του πεδίου ορισμού της ,αν το όριο υπάρχει και είναι πραγματικός αριθμός .
.
18.Έστω η συνάρτηση f με πεδίο ορισμού το Α. Πώς ορίζεται η (πρώτη) παράγωγος της f; Απάντηση Αν Β είναι το σύνολο των x∈A στα οποία η f είναι παραγωγίσιμη τότε ορίζεται μια νέα συνάρτηση, με την οποία κάθε x∈B αντιστοιχίζεται στο Η συνάρτηση αυτή λέγεται (πρώτη) παράγωγος της f και συμβολίζεται με f΄. Αντίστοιχα η παράγωγος της συνάρτησης f΄ λέγεται δεύτερη παράγωγος της f και συμβολίζεται με f΄΄.
.
19.Έστω f μια συνάρτηση και A(x0 , f (x0 )) ένα σημείο της γραφικής της παράστασης C. Ποιος είναι ο συντελεστής διεύθυνσης της εφαπτομένης της C στο Α; Απάντηση
.
20.Τι ονομάζεται ρυθμός μεταβολής του y = f (x) ως προς το x, όταν x = x0 ; Απάντηση
Ρυθμός μεταβολής του y = f (x) ως προς το x, όταν x = x0 ονομάζεται η παράγωγος της f στο x0 , δηλαδη το f ΄(x0).
21.Τι ορίζουμε στιγμιαία ταχύτητα ενός κινητού; Απάντηση
Την οριακή τιμή της μέσης ταχύτητας ενός κινητού την ονομάζουμε στιγμιαία ταχύτητα του κινητού στη χρονική στιγμή t0 ή απλώς ταχύτητα του κινητού στο t0, δηλαδή .
22.Να αποδείξετε ότι η παράγωγος της σταθερής συνάρτησης f(x) = c, όπου c πραγματική σταθερά, ισούται με μηδέν , δηλαδη (c)΄= 0 . Απάντηση
Έχουμε f(x + h) – f(x) = c – c = 0 και για h ≠ 0 , , οπότε και
. Άρα (c)΄= 0 .
23.Να αποδείξετε ότι η παράγωγος της ταυτοτικής συνάρτησης f (x) = x είναι ίση με 1 ,δηλαδή ότι (x)′ = 1. Απάντηση Για h ≠ 0 έχουμε: Επομένως
Έχουμε f(x + h) – f(x) = (x + h) – x = h . .
. Άρα (x)΄ = 1 .
24. Να αποδείξετε ότι η παράγωγος της συνάρτησης f (x) = x2 είναι 2x δηλαδή ότι (x2 )′ = 2x . Απάντηση Έστω η συνάρτηση f (x) = x2. Έχουμε f (x + h) − f (x) = (x + h)2 − x2 = x2 + 2x·h + h2 − x2 = (2x + h)·h . Για h ≠ 0 , είναι Επομένως, Άρα (x2 )′ = 2x .
.
.
25.Αν η συνάρτηση f είναι παραγωγίσιμη στο ℝ και c είναι μια πραγματική σταθερά, να δείξετε ότι: (c·f(x))΄= c·f΄(x) , x∈ℝ. Απάντηση Έχουμε F (x + h) − F (x) = c·f(x+ h) – c·f(x) = c[f(x + h) – f(x)]. Για h ≠ 0 έχουμε: Επομένως Άρα (c·f(x))΄= c·f΄(x) .
Έστω F(x) = c·f(x) . .
.
26.Αν οι συναρτήσεις f και g είναι παραγωγίσιμες να δείξετε ότι: (f(x) + g(x))΄= f΄(x) + g΄(x) . Απάντηση Έχουμε F (x + h) − F (x) = [f(x+ h) + g(x + h) ] – [f(x) + g(x)] = [f(x + h) – f(x)] + [g(x + h) – g(x)]. Για h ≠ 0 έχουμε: Επομένως f΄(x) + g΄(x) . Άρα (f(x) + g(x))΄= f΄(x) + g΄(x) .
Έστω η συνάρτηση F(x) = f(x) + g(x) .
.
27.Να γράψετε τις παραγώγους των βασικών συναρτήσεων και τους κανόνες παραγώγισης. Απάντηση
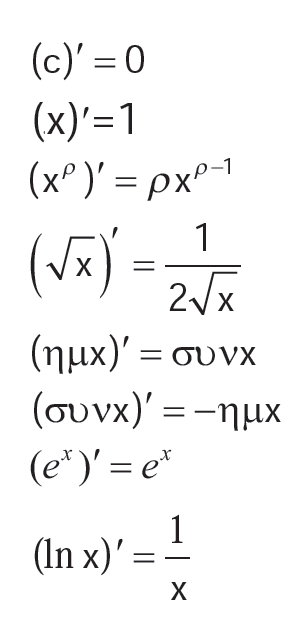

28.Αν μία συνάρτηση f είναι παραγωγίσιμη σε ένα διάστημα Δ και ισχύει f ′(x) > 0 (αντιστοίχως f ′(x) < 0 ) για κάθε εσωτερικό σημείο του Δ τι συμπέραίνουμε για την μονοτονία της στο Δ ; Απάντηση Αν μία συνάρτηση f είναι παραγωγίσιμη σε ένα διάστημα Δ και ισχύει f ′(x) > 0 (αντιστοίχως f ′(x) < 0) για κάθε εσωτερικό σημείο του Δ τότε η f είναι γνησίως αύξουσα (αντιστοίχως γνησίως φθίνουσα) στο Δ .
Απάντηση ΣΧΟΛΙΟ Αν για τη συνάρτηση f ισχύουν f ′ (x0) = 0 για x0∈ (α , β) ,και η παράγωγος της f΄ διατηρεί πρόσημο εκατέρωθεν του x0 , τότε η f είναι γνησίως μονότονη στο (α , β) και δεν παρουσιάζει ακρότατα στο διάστημα αυτό.
Αν για τη συνάρτηση f ισχύουν f ′ (x0) = 0 για x0∈ (α , β) , f ′(x) > 0 στο (α , x0 ) και f ′(x) < 0 στο (x0 , β) (αντίστοιχα f ′ (x0) = 0 για x0∈ (α, β) , f ′(x) < 0 στο (α , x0 ) και f ′(x) > 0 στο (x0 , β) ) τότε η f παρουσιάζει στο διάστημα (α , β) μέγιστο για x = x0 (αντιστοίχως η f παρουσιάζει ελάχιστο στο διάστημα (α , β) για x = x0 ).
