28.Τι ονομάζουμε συντελεστή διεύθυνσης ενός διανύσματος Απάντηση Έστω Το πηλίκο Επομένως: ΣΧΟΛΙΑ Είναι φανερό ότι: →Αν y = 0, δηλαδή αν →Αν x = 0 , δηλαδή αν ;
ένα μη μηδενικό διάνυσμα.
της τεταγμένης προς την τετμημένη του διανύσματος
, με x ≠ 0, το λέμε συντελεστή διεύθυνσης του
και τον συμβολίζουμε με
ή απλώς με λ.
.
// x΄x, τότε ο συντελεστής διεύθυνσης του διανύσματος
είναι ο λ = 0.
// y΄y, τότε δεν ορίζεται συντελεστής διεύθυνσης του διανύσματος
.
Απάντηση Έστω δύο διανύσματα Τότε έχουμε τις ισοδυναμίες: Επομένως, η συνθήκη παραλληλίας για δύο διανύσματα και
,δύο διανύσματα με συντελεστές διεύθυνσης λ1 και λ2 αντιστοίχως ,τότε
.
και
, με συντελεστές διεύθυνσης λ1 και λ2 αντιστοίχως.
και
, με συντελεστές διεύθυνσης λ1 και λ2 διατυπώνεται ως εξής:
.
Απάντηση Ονομάζουμε εσωτερικό γινόμενο δύο μη μηδενικών διανυσμάτων Aν ΣΧΟΛΙΑ Άμεσες συνέπειες του παραπάνω ορισμού είναι οι εξής: και
;
και
και το συμβολίζουμε με
tον πραγματικό αριθμό
,όπου φ η γωνία των διανυσμάτων
και
.
ή
, τότε ορίζουμε
.


Απάντηση “Το εσωτερικό γινόμενο δύο διανυσμάτων είναι ίσο με το άθροισμα των γινομένων των ομώνυμων συντεταγμένων τους”. Δηλαδή αν δύο διανύσματα και
.

και
, τότε το εσωτερικό τους γινόμενο είναι ίσο με
.
Απάντηση Aν .(Επιμεριστική Ιδιότητα)
,
και
τότε έχουμε:
Απάντηση Aν Είναι όμως Επομένως ,
και θ η γωνία που σχηματίζουν τότε να αποδείξετε οτι
.
,
είναι δύο μη μηδενικά διανύσματα του επιπέδου που σχηματίζουν γωνία θ, τότε
και επομένως ,
.
,
.
Απάντηση Έστω Με αρχή ένα σημείο Ο παίρνουμε τα διανύσματα Το διάνυσμα Δηλαδή, Αποδεικνύεται ότι η προβολή του δύο διανύσματα του επιπέδου με
.Τι ονομάζουμε προβολή του διανύσματος
στο διάνυσμα
;
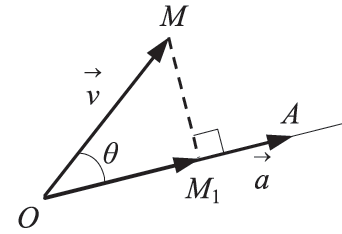
δύο διανύσματα του επιπέδου με
.
και
.Από το Μ φέρνουμε κάθετο στη διεύθυνση του
και έστω Μ1 το ίχνος της καθέτου.
λέγεται προβολή του διανύσματος
στο διάνυσμα
και συμβολίζεται με
.
.
πάνω στο
είναι ανεξάρτητη από την επιλογή του σημείου Ο.
Απάντηση Έστω Φέρνουμε τη προβολή του διανύσματος .

δύο διανύσματα του επιπέδου με
.
στο διάνυσμα
δηλαδή το διάνυσμα
και έχουμε:
