Απάντηση

Μια εξίσωση με δύο αγνώστους x, y λέγεται εξίσωση μιας γραμμής C, όταν οι συντεταγμένες των σημείων της C, και μόνο αυτές, την επαληθεύουν.

Απάντηση

Έστω Οxy ένα σύστημα συντεταγμένων στο επίπεδο και ε μια ευθεία που τέμνει τον άξονα x′x στο σημείο Α.

Τη γωνία ω που διαγράφει ο άξονας x′x όταν στραφεί γύρω από το Α κατά τη θετική φορά  μέχρι να συμπέσει με την ευθεία ε τη λέμε γωνία που σχηματίζει η ε με τον άξονα x΄x.

Αν η ευθεία ε είναι παράλληλη προς τον άξονα x΄x, τότε λέμε ότι σχηματίζει με αυτόν γωνία ω = 0 .

Σε  κάθε περίπτωση για τη γωνία ω ισχύει 0^ο ≤ ω < 180^ο ή σε ακτίνια 0 ≤ ω < π.

Απάντηση

Ως  συντελεστή διεύθυνσης ή ως κλίση μιας ευθείας ε ορίζουμε την εφαπτομένη της  γωνίας ω που σχηματίζει η ε με τον άξονα x′x.

Προφανώς ο συντελεστής διεύθυνσης μιας ευθείας είναι θετικός, αν η γωνία ω που σχηματίζει με τον άξονα x΄x είναι οξεία και αρνητικός, αν είναι αμβλεία.  

Αν η ευθεία σχηματίζει με τον x΄x μηδενική γωνία, δηλαδή είναι παράλληλη στον άξονα x′x, ο συντελεστής διεύθυνσης είναι ίσος με μηδέν.

Στην περίπτωση που η γωνία της ευθείας ε με τον άξονα x′x είναι 90^ο, δηλαδή η ευθεία ε είναι κάθετη στον άξονα x′x, δεν ορίζουμε συντελεστή διεύθυνσης για την ευθεία αυτή.

Απάντηση

Έστω ένα διάνυσμα    παράλληλο σε μια ευθεία ε. Αν φ και ω είναι οι γωνίες που σχηματίζουν το   και η ε με τον x′x αντιστοίχως, τότε θα ισχύει φ = ω ή φ = π + ω  και επομένως εφφ = εφω .

Άρα όταν μια ευθεία και ένα διάνυσμα είναι είναι παράλληλα, έχουν τον ίδιο συντελεστή διεύθυνσης.

5.Να αποδείξετε ότι o συντελεστής διεύθυνσης λ μιας ευθείας που διέρχεται από τα σημεία A(x₁ , y₁) και B(x₂ , y₂) ,με x₁ ≠ x₂ , είναι  .

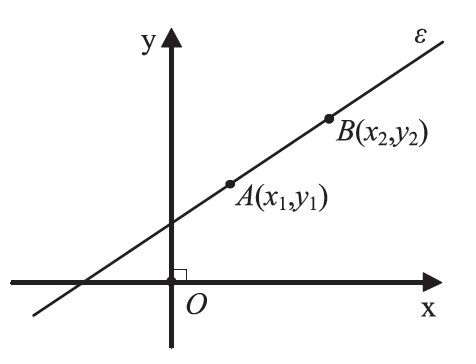
Απάντηση

Αν είναι γνωστές οι συντεταγμένες δύο σημείων μιας μη κατακόρυφης ευθείας ε, δηλαδή μιας ευθείας που δεν είναι κάθετη στον άξονα x′x, τότε μπορούμε να βρούμε και το συντελεστή διεύθυνσης της ευθείας αυτής.

Πράγματι, αν A(x₁ , y₁) και B(x₂ , y₂)  είναι δύο σημεία της ευθείας ε, τότε ο συντελεστής διεύθυνσης της ε είναι ίσος με το συντελεστή διεύθυνσης του διανύσματος , δηλαδή ίσος με  .

Απάντηση

Έστω οι ευθείες ε₁ και ε₂ με αντίστοιχους συντελεστές διεύθυνσης  λ₁ και λ₂ , και τα διανύσματα  και   είναι παράλληλα προς τις ε₁ και ε₂ αντιστοίχως, έχουμε τις ισοδυναμίες:

  και    .

Απάντηση

Έστω Οxy ένα σύστημα συντεταγμένων στο επίπεδο και Α(x₀ , y₀)  ένα σημείο του επιπέδου.

Ένα σημείο M(x , y) διαφορετικό του Α(x₀ , y₀)  ανήκει στην ε, αν και μόνο αν το διάνυσμα    είναι παράλληλο στην ε, δηλαδή αν και μόνο αν το    και η ε έχουν τον ίδιο συντελεστή διεύθυνσης.

Επειδή , έχουμε .
Επομένως, το σημείο M(x , y) ανήκει στην ε αν και μόνο αν    ή .
Η τελευταία εξίσωση επαληθεύεται και από το σημείο Α(x₀ , y₀) .

Άρα η εξίσωση της ευθείας ε είναι:   .

8.Nα αποδείξετε οτι αν A(x₁ , y₁) και B(x₂ , y₂) ,με x₁ ≠ x₂ ,σημεία του επιπέδου τότε η εξίσωση της ευθείας ε που διέρχεται από τα Α και Β είναι  . 

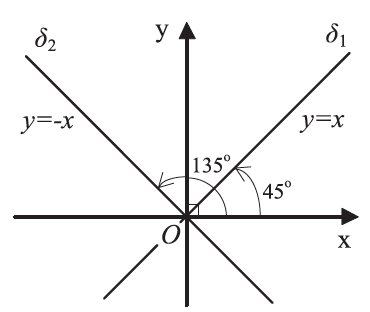
Απάντηση

Έστω ε η ευθεία που διέρχεται από τα σημεία Α(x₁ , y₁) και Β(x₂ , y₂) με x₁ ≠ x₂ .

Ο συντελεστής διεύθυνσης της ευθείας είναι    και επομένως η εξίσωση  γίνεται   .

ΣΧΟΛΙΑ

Οι εξισώσεις    και   δεν μπορούν να χρησιμοποιηθούν, όταν η ευθεία ε είναι κατακόρυφη, αφού στην περίπτωση αυτή δεν ορίζεται ο συντελεστής διεύθυνσης της ευθείας.

Όμως η εξίσωση μιας κατακόρυφης ευθείας που διέρχεται απο το σημείο Α(x₀ , y₀) μπορεί να βρεθεί αμέσως, αφού κάθε σημείο της Μ έχει τετμημένη x₀ και άρα η εξίσωσή της είναι: x = x₀ .

Ειδικές περιπτώσεις

→Η εξίσωση ευθείας που τέμνει τον άξονα y′y στο σημείο A(0 , β) και έχει συντελεστή διεύθυνσης λ είναι y – β = λ(x – 0) , η οποία τελικά γράφεται y = λx + β .

→Αν μια ευθεία διέρχεται από την αρχή των αξόνων και έχει συντελεστή διεύθυνσης λ, τότε η εξίσωσή της είναι y – 0 = λ(x – 0) ή y = λx .

→Oι διχοτόμοι των γωνιών xOy και yOx΄ έχουν εξισώσεις y = x και y = −x  αντιστοίχως.

→Aν μια ευθεία διέρχεται από το σημείο Α(x₀ , y₀) και είναι παράλληλη στον άξονα x′x, δηλαδή είναι όπως λέμε μια οριζόντια ευθεία, έχει εξίσωση y – y₀ = 0(x – x₀) ,δηλαδή y = y₀ .

Απάντηση

Έστω ε μια ευθεία στο καρτεσιανό επίπεδο.

 Αν η ευθεία ε τέμνει τον άξονα yy′ στο σημείο Σ(0 , β) και έχει συντελεστή διεύθυνσης λ, τότε θα έχει εξίσωση y = λx + β . η οποία γράφεται  λx + (-1)y +β = 0 .

 Αν η ευθεία ε είναι κατακόρυφη και διέρχεται από το σημείο P(x₀ , y₀) , τότε θα έχει εξίσωση

x = x₀ , η οποία γράφεται ισοδύναμα x + 0y +(-x₀) = 0 .

Βλέπουμε, δηλαδή, ότι και στις δύο περιπτώσεις η εξίσωση της ευθείας ε παίρνει τη μορφή

Ax + By + Γ  = 0 με A ≠ 0 ή  B ≠ 0.

ΑΝΤΙΣΤΡΟΦΩΣ

Έστω η εξίσωση Ax + By + Γ  = 0 με A ≠ 0 ή  B ≠ 0.

• Αν B ≠ 0, τότε η εξίσωση γράφεται , που είναι εξίσωση ευθείας με συντελεστή   και η οποία τέμνει τον άξονα yy′ στο σημείο .

• Αν B = 0, τότε, λόγω της υπόθεσης, είναι A ≠ 0 και η εξίσωση γράφεται , που είναι εξίσωση ευθείας κάθετης στον άξονα x′x στο σημείο του .

Σε όλες λοιπόν τις περιπτώσεις η εξίσωση Ax + By + Γ  = 0 με A ≠ 0 ή  B ≠ 0 ,παριστάνει ευθεία.

10.Να αποδείξετε ότι η ευθεία με εξίσωση Ax + Βy + Γ = 0 είναι παράλληλη στο διάνυσμα  και κάθετη στο διάνυσμα  .

Απάντηση

Έστω Οxy ένα σύστημα συντεταγμένων στο επίπεδο και ε μια ευθεία του επιπέδου με εξίσωση

Ax + By + Γ  = 0. Είδαμε προηγουμένως ότι:

Αν B ≠ 0, τότε η ε έχει συντελεστή διεύθυνσης    και επομένως είναι παράλληλη στο διάνυσμα  .

Αν B = 0, τότε η ε είναι παράλληλη προς τον άξονα yy′ και επομένως παράλληλη και πάλι προς το διάνυσμα  .

Σε κάθε περίπτωση λοιπόν ισχύει ότι:

Η ευθεία με εξίσωση Ax + Βy + Γ = 0 είναι παράλληλη στο διάνυσμα  .

Όμως, το διάνυσμα  είναι κάθετο στο διάνυσμα   , αφού:

  .

Eπομένως:

Η ευθεία με εξίσωση Ax + Βy + Γ = 0 είναι κάθετη στο διάνυσμα  .

Απάντηση

Έστω ε μια ευθεία του καρτεσιανού επιπέδου, με εξίσωση Ax + Βy + Γ = 0 και M₀(x₀ , y₀) ένα σημείο εκτός αυτής. 

Η απόσταση d(M₀ , ε) του σημείου Μ₀ από την ευθεία ε δίνεται απο τον παρακάτω τύπο:

Απάντηση

Έστω Α(x₁ , y₁)  , B(x₂ , y₂) και Γ(x₃ , y₃) τρία σημεία του καρτεσιανού επιπέδου.

Το εμβαδόν του τριγώνου ΑΒΓ δίνεται απο τον παρακάτω τύπο: