μονωνυμα

No comments

Συνοπτική θεωρία

Aλγεβρικές παραστάσεις

  • Αριθμητική παράσταση ονομάζεται η παράσταση που περιέχει πράξεις μεταξύ αριθμών.
  • Αλγεβρική λέγεται η παράσταση η οποία περιέχει πράξεις μεταξύ αριθμών και μεταβλητών.
  • Μια αλγεβρική παράσταση λέγεται ακέραια όταν μεταξύ των μεταβλητών της σημειώνονται μόνο οι πράξεις της πρόσθεσης και του πολλαπλασιασμού και οι εκθέτες των μεταβλητών είναι θετικοί ακέραιοι.

Οι παραστάσεις  -3x+7y^3 , \frac{1}{3}a^4\beta -\sqrt{2}\omega , 4\alpha ^{2 }-2\alpha \beta   λέγονται ακέραιες αλγεβρικές παραστάσεις.

  • Αν αντικαταστήσουμε τις μεταβλητές με αριθμούς και κάνουμε τις πράξεις τότε προκύπτει ένας αριθμός που λέγεται αριθμητική τιμή της αλγεβρικής παράστασης.

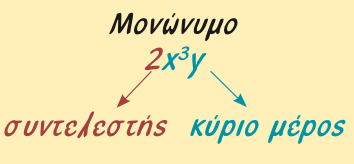
Η αριθμητική τιμή της παράστασης 4\alpha ^{2 }-2\alpha \beta   για α=-1 και β=3 είναι 4\left ( -1 \right ) ^{2 }-2\left ( -1 \right ) \cdot 3=4\cdot 1+6=4+6=10

Μονώνυμα

  • Μονώνυμο ονομάζεται η ακέραια αλγεβρική παράσταση που οι αριθμοί και οι μεταβλητές συνδέονται μόνο με τη πράξη του πολλαπλασιασμού.

πχ 5z^{2}x^{3} , -\sqrt{5}a\beta ^{5} , \frac{4}{5}xya^{2}

  • Ο αριθμητικός παράγοντας, που συνήθως γράφεται πρώτος, λέγεται συντελεστής του μονωνύμου ενώ το γινόμενο των μεταβλητών λέγεται κύριο μέρος του μονωνύμου.

  • Βαθμός του μονωνύμου ως προς μια μεταβλητή λέγεται ο εκθέτης της μεταβλητής αυτής.
  • Βαθμός του μονωνύμου ως προς όλες τις μεταβλητές του λέγεται το άθροισμα των εκθετών των μεταβλητών του.

  • ∆υο ή περισσότερα μονώνυμα που έχουν το ίδιο κύριο μέρος λέγονται όμοια μονώνυμα.

πχ τα μονώνυμα  -\sqrt{3}a^{2}\beta ^{3} ,2a^{2}\beta ^{3},-6a^{2}\beta ^{3},\frac{8}{13}a^{2}\beta ^{3} είναι μεταξύ τους όμοια.

  • Ίσα λέγονται τα όμοια μονώνυμα που έχουν τον ίσους συντελεστές.
  • Αντίθετα λέγονται τα όμοια μονώνυμα που έχουν αντίθετους συντελεστές.
  • Σταθερό μονώνυμο λέμε οποιοδήποτε πραγματικό αριθμό.
  • Μηδενικό μονώνυμο λέμε τον (σταθερό μονώνυμο) αριθμό μηδέν 0 και για το οποίο δεν ορίζεται βαθμός.
  • Κάθε μη μηδενικό και σταθερό μονώνυμο είναι μηδενικού βαθμού.

ΠΡΑΞΕΙΣ ΜΕ ΜΟΝΩΝΥΜΑ

  • Το άθροισμα όμοιων μονωνύμων είναι ένα μονώνυμο όμοια με αυτά και έχει συντελεστή το άθροισμα των συντελεστών τους.
  • Το γινόμενο μονωνύμων είναι ένα μονώνυμο με συντελεστή το γινόμενο των συντελεστών τους και κύριο μέρος το γινόμενο όλων των μεταβλητών τους με εκθέτη κάθε μεταβλητής το άθροισμα των εκθετών της.

ΧΡΗΣΙΜΕΣ ΙΔΙΟΤΗΤΕΣ ΓΙΑ ΤΟ ΓΙΝΟΜΕΝΟ ΜΟΝΩΝΥΜΩΝ

\alpha ^{\kappa} \cdot \alpha ^{\lambda }=\alpha ^{\kappa+\lambda }

(\alpha ^{\kappa}) ^{\lambda }=\alpha ^{\kappa\cdot \lambda }

  • Η διαίρεση μονωνύμων γίνεται όπως και η διαίρεση αριθμών. Το πηλίκο δύο μονωνύμων δεν είναι πάντα μονώνυμο.

     

    ΧΡΗΣΙΜΕΣ ΙΔΙΟΤΗΤΕΣ ΓΙΑ ΤΟ ΠΗΛΙΚΟ ΜΟΝΩΝΥΜΩΝ

    \frac{\alpha ^{\kappa }}{\alpha ^{\lambda }}= {\alpha ^{\kappa-\lambda }}

     

    (download)  ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ 

     

    Eπαναληπτικό quiz