Εξισώσεις
Απάντηση αx + β = 0 ⇔ αx + β – β = -β ⇔ αx = -β (1) Διακρίνουμε τώρα τις περιπτώσεις: →Αν α ≠ 0 τότε: (1) αx = -β⇔ x = Επομένως, αν α ≠ 0 η εξίσωση έχει ακριβώς μία λύση, την x = →Αν α = 0 , τότε : Αν είναι β ≠ 0 η εξίσωση (1) δεν έχει λύση και γι αυτό λέμε ότι είναι αδύνατη, ενώ αν είναι β = 0 η εξίσωση (1) έχει τη μορφή 0x = 0 και αληθεύει για κάθε πραγματικό αριθμό x, δηλαδή είναι ταυτότητα. Η λύση της εξίσωσης αx + β = 0 και γενικά κάθε εξίσωσης λέγεται και ρίζα αυτής.
.
.
Απάντηση Η εξίσωση xν = α , με α > 0 και ν περιττό φυσικό αριθμό, έχει ακριβώς μια λύση, την Η εξίσωση xν = α ,με α > 0 και ν άρτιο φυσικό αριθμό, έχει ακριβώς δύο λύσεις, τις Η εξίσωση xν = α, με α < 0 και ν περιττό φυσικό αριθμό, έχει ακριβώς μια λύση, την Η εξίσωση xν = α , με α < 0 και ν άρτιο φυσικό αριθμό, είναι αδύνατη. ΣΧΟΛΙΟ Από τα παραπάνω συμπεράσματα και από το γεγονός ότι η εξίσωση xν = αν, με ν∈ℕ*, έχει προφανή λύση τη x = α, προκύπτει ότι: Αν ο ν περιττός, τότε η εξίσωση xν = αν έχει μοναδική λύση, τη x = α. Αν ο ν άρτιος, τότε η εξίσωση xν = αν έχει δύο λύσεις, τις x1 = α και x2 = – α.
.
και
.
.
Απάντηση Έχουμε: Αν θέσουμε Δ = β2 ‒ 4αγ, τότε η τελευταία εξίσωση γίνεται: Διακρίνουμε τώρα τις εξής περιπτώσεις: Επομένως η εξίσωση (2), άρα και η ισοδύναμή της (1), έχει δύο λύσεις άνισες, τις: Για συντομία οι λύσεις αυτές γράφονται Στην περίπτωση αυτή λέμε ότι η εξίσωση έχει διπλή ρίζα την ΣΧΟΛΙΟ Η αλγεβρική παράσταση Δ = β2 ‒ 4αγ, από την τιμή της οποίας εξαρτάται το πλήθος των ριζών της εξίσωσης αx2 + βx + γ = 0, α ≠ 0, ονομάζεται διακρίνουσα αυτής.
(2)
ή
δηλαδή
ή
και
.
ή
ή
.
Τα παραπάνω συμπεράσματα συνοψίζονται στον ακόλουθο πίνακα:
Απάντηση Στην περίπτωση που η εξίσωση αx2 + βx + γ = 0, α ≠ 0 έχει πραγματικές ρίζες x1, x2, έχουμε: Αν με S συμβολίσουμε το άθροισμα x1 + x2 και με P το γινόμενο x1 · x2, τότε έχουμε τους τύπους: ΣΧΟΛΙΟ Η εξίσωση αx2 + βx + γ = 0, α ≠ 0 με τη βοήθεια των τύπων του Vieta, μετασχηματίζεται ως εξής: Η τελευταία μορφή της εξίσωσης αx2 + βx + γ = 0 μας δίνει τη δυνατότητα να την κατασκευάσουμε, όταν γνωρίζουμε το άθροισμα και το γινόμενο των ριζών της. και
(Τύποι Vieta).
και
.
και
που είναι γνωστοί ως τύποι του Vieta.
.
Ανισώσεις
Απάντηση αx + β > 0 ⇔ αx + β – β > -β ⇔ αx > -β (1) Διακρίνουμε τώρα τις περιπτώσεις: →Αν α > 0 τότε: (1) αx > -β⇔ x > →Αν α < 0 τότε: (1) αx > -β⇔ x < Αν α = 0, τότε η ανίσωση γίνεται 0x > ‒ β,
.
.
Απάντηση Το τριώνυμο αx2+βx+γ ,(α≠0) μετασχηματίζεται ως εξής: Επομένως: Διακρίνουμε τώρα τις εξής περιπτώσεις: Επομένως: αx2 + βx + γ = α(x ‒ x1)(x ‒ x2), όπου x1, x2 οι ρίζες του τριωνύμου. Άρα, όταν Δ > 0, τότε το τριώνυμο μετατρέπεται σε γινόμενο του α επί δύο πρωτοβάθμιους παράγοντες. Άρα, όταν Δ = 0, τότε το τριώνυμο μετατρέπεται σε γινόμενο του α επί ένα τέλειο τετράγωνο. Επειδή για κάθε x∈ℝ , η παράσταση μέσα στην αγκύλη είναι θετική, το τριώνυμο δεν αναλύεται σε γινόμενο πρωτοβάθμιων παραγόντων. Συνοψίζοντας τα παραπάνω συμπεράσματα για τις μορφές του τριωνύμου αx2 + βx + γ, α ≠ 0 με διακρίνουσα Δ έχουμε:
.
. (1)
, οπότε έχουμε:
.
.
.
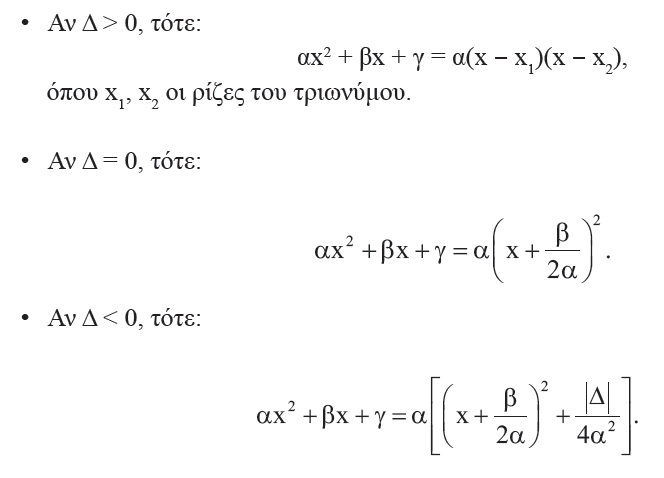
Απάντηση Για να μελετήσουμε το πρόσημο των τιμών του τριωνύμου αx2 + βx + γ, α ≠ 0, θα χρησιμοποιήσουμε τις μορφές του ανάλογα με τη διακρίνουσα. →Αν Δ > 0, τότε ισχύει: αx2 + βx + γ = α (x ‒ x1 )(x ‒ x2) (1) Υποθέτουμε ότι x1 < x2 και τοποθετούμε τις ρίζες σε έναν άξονα. Παρατηρούμε ότι: →Αν Δ = 0, τότε ισχύει: Επομένως, το τριώνυμο είναι ομόσημο του α για κάθε πραγματικό →Αν Δ < 0, τότε ισχύει: Όμως η παράσταση μέσα στην αγκύλη είναι θετική για κάθε πραγματικό αριθμό x. Επομένως το τριώνυμο είναι ομόσημο του α σε όλο το ℝ. Συνοψίζοντας τα παραπάνω έχουμε : Το τριώνυμο αx2 + βx + γ, α ≠ 0 γίνεται:
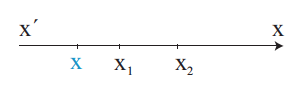
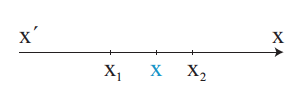
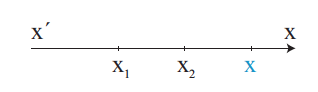
.
, ενώ μηδενίζεται για
.
.
