Απάντηση

Συνάρτηση από ένα σύνολο Α σε ένα σύνολο Β λέγεται μια διαδικασία (κανόνας) με την οποία κάθε στοιχείο του συνόλου Α αντιστοιχίζεται σε ένα ακριβώς στοιχείο του συνόλου Β.

ΣΧΟΛΙΑ

• Το σύνολο Α λέγεται πεδίο ορισμού ή σύνολο ορισμού της ƒ.
• Αν με μια συνάρτηση ƒ από το Α στο Β, το x∈Α αντιστοιχίζεται στο y∈Β , τότε γράφουμε: y = ƒ(x) .
• Το ƒ(x) λέγεται τότε τιμή της ƒ στο x. Το γράμμα x, που παριστάνει οποιοδήποτε στοιχείο του πεδίου ορισμού της ƒ, ονομάζεται ανεξάρτητη μεταβλητή, ενώ το y, που παριστάνει την τιμή της συνάρτησης στο x, ονομάζεται εξαρτημένη μεταβλητή.
• Το σύνολο, που έχει για στοιχεία του τις τιμές ƒ(x) για όλα τα x∈Α, λέγεται σύνολο τιμών της ƒ και το συμβολίζουμε με ƒ(Α).

Απάντηση

• Tο συμμετρικό του A(α , β) ως προς τον άξονα x′x είναι το σημείο Δ(α,‒β), που έχει ίδια τετμημένη και αντίθετη τεταγμένη .
• Το συμμετρικό του A(α , β) ως προς τον άξονα y′y είναι το σημείο Β(‒α,β), που έχει ίδια τεταγμένη και αντίθετη τετμημένη .  
• Το συμμετρικό του A(α , β) ως προς την αρχή των αξόνων είναι το σημείο Γ(‒α,‒β), που έχει αντίθετες συντεταγμένες .

• Το συμμετρικό του A(α , β) ως προς τη διχοτόμο της 1ης και 3ης γωνίας των αξόνων (y = x),είναι το σημείο  Α′(β,α) που έχει τετμημένη την τεταγμένη του Α και τεταγμένη την τετμημένη του Α .

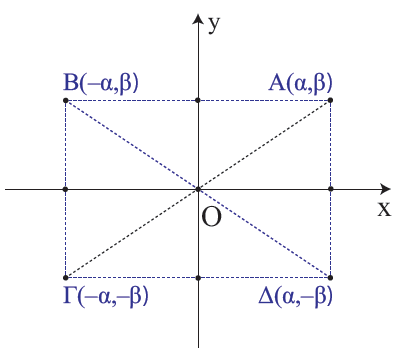
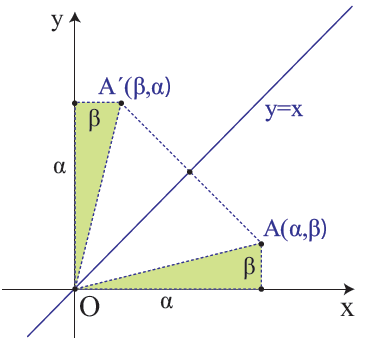
3.Τι ονομάζουμε γραφική παράσταση μιας συνάρτησης; 

Απάντηση

Έστω ƒ μια συνάρτηση με πεδίο ορισμού Α και Oxy ένα σύστημα συντεταγμένων στο επίπεδο. Το σύνολο των σημείων M(x, y) για τα οποία ισχύει y = ƒ(x), δηλαδή το σύνολο των σημείων M(x, ƒ(x)), x∈A, λέγεται γραφική παράσταση της ƒ και συμβολίζεται συνήθως με C_ƒ.

ΣΧΟΛΙΑ

Η εξίσωση, λοιπόν, y = ƒ(x) επαληθεύεται από τα σημεία της C_ƒ και μόνο από αυτά. Επομένως, η y = ƒ(x) είναι η εξίσωση της γραφικής παράστασης της ƒ. Για το λόγο αυτό, τη γραφική παράσταση C_ƒ της ƒ τη συμβολίζουμε, πολλές φορές, απλά με την εξίσωσή της, δηλαδή με y = ƒ(x).

Επειδή κάθε x∈A αντιστοιχίζεται σε ένα μόνο y∈ℝ, δεν υπάρχουν σημεία της γραφικής παράστασης της ƒ με την ίδια τετμημένη. Αυτό σημαίνει ότι κάθε κατακόρυφη ευθεία έχει με τη γραφική παράσταση της ƒ το πολύ ένα κοινό σημείο . Έτσι, ο κύκλος δεν αποτελεί γραφική παράσταση συνάρτησης.

Όταν δίνεται η γραφική παράσταση μιας συνάρτησης ƒ μπορούμε, επίσης, να σχεδιάσουμε και τη γραφική παράσταση της συνάρτησης ‒ƒ, παίρνοντας τη συμμετρική της γραφικής παράστασης της ƒ ως προς τον άξονα x′x και τούτο διότι η γραφική παράσταση της ‒ƒ αποτελείται από τα σημεία M′(x, ‒ƒ(x)) που είναι συμμετρικά των σημείων M(x, ƒ(x)) της γραφικής παράστασης της ƒ ως προς τον άξονα x′x.

4.Έστω Oxy ένα σύστημα συντεταγμένων στο επίπεδο και Α(x₁,y₁) και B(x₂,y₂) δύο σημεία αυτού.Nα αποδείξετε ότι η απόστασή τους δίνεται από τον τύπο:   .

Απάντηση

Από το ορθογώνιο τρίγωνο KAB του παρακάτω σχήματος έχουμε:

(ΑΒ)² = (ΚΑ)² + (ΚΒ)² =  |x₂ – x₁|² + |y₂ – y₁|² = (x₂ – x₁)² + (y₂ – y₁)² ,οπότε  .

Ο παραπάνω τύπος ισχύει και στην περίπτωση που η ΑΒ είναι παράλληλη με τον άξονα x′x  ή παράλληλη με τον άξονα y′y .

Απάντηση

Ως συντελεστή διεύθυνσης ή ως κλίση μιας ευθείας ε ορίζουμε την εφαπτομένη της γωνίας ω που σχηματίζει η ε με τον άξονα x′x.

ΣΧΟΛΙΑ

Ο συντελεστής διεύθυνσης μιας ευθείας ε συμβολίζεται συνήθως με λε ή απλά με λ. Είναι φανερό ότι:

Ο συντελεστής διεύθυνσης της ευθείας ε είναι θετικός, αν η γωνία ω είναι οξεία,

αρνητικός, αν η γωνία ω είναι αμβλεία και

μηδέν, αν η γωνία ω είναι μηδέν.

Στην περίπτωση που η γωνία ω είναι ίση με 90°, δηλαδή όταν η ευθεία ε είναι κάθετη στον άξονα x′x, δεν ορίζουμε συντελεστή διεύθυνσης για την ε.

6.Τι γνωρίζετε για τη γραφική παράσταση της ƒ(x) = αx + β ;

Απάντηση

Η γραφική παράσταση της συνάρτησης  ƒ(x) = αx + β είναι μία ευθεία, με εξίσωση y = αx + β, η οποία τέμνει τον άξονα των y στο σημείο Β(0,β) και έχει κλίση λ = α .

Είναι φανερό ότι:

• Αν α > 0, τότε 0° < ω < 90°.
• Αν α < 0, τότε 90° < ω < 180°.
• Αν α = 0, τότε ω = 0°.

Στην περίπτωση που είναι α = 0, η συνάρτηση παίρνει τη μορφή ƒ(x) = β και λέγεται σταθερή συνάρτηση, διότι η τιμή της είναι η ίδια για κάθε x∈ℝ.

7.Έστω δύο τυχαία σημεία A(x₁,y₁) και B(x₂,y₂) της ευθείας  y = αx + β. Να αποδείξετε οτι η κλίση α της ευθείας ισούται με   .

Απάντηση

Έστω δύο τυχαία σημεία A(x₁,y₁) και B(x₂,y₂) της ευθείας  y = αx + β.

Τότε θα ισχύει: y₁ = αx₁ + β και y₂ = αx₂ + β  οπότε θα έχουμε: 

y₂ – y₁ = (αx₂ + β) – (αx₁ + β) = α(x₂ – x₁) .

Επομένως θα είναι   .

Απάντηση

Έστω δύο ευθείες ε₁ και ε₂ με εξισώσεις y = α₁x + β₁ και y = α₂x + β₂ αντίστοιχα και ας υποθέσουμε ότι οι ευθείες αυτές σχηματίζουν με τον άξονα x′x γωνίες ω₁ και ω₂ αντιστοίχως.

• Αν α₁ = α₂, τότε εφω₁ = εφω₂, οπότε ω₁= ω₂ και άρα οι ευθείες ε₁ και ε₂ είναι παράλληλες ή συμπίπτουν.

Ειδικότερα:
→Αν α₁ = α₂ και β₁ ≠ β₂, τότε οι ευθείες είναι παράλληλες .

→Αν α₁ = α₂ και β₁ = β₂, τότε οι ευθείες ταυτίζονται.

• Αν α₁ ≠ α₂ , τότε εφω₁ ≠ εφω₂ , οπότε ω₁ ≠ ω₂ και άρα οι ευθείες ε₁ και ε₂ τέμνονται.