18.Πως ορίζεται η αντίστροφη συνάρτηση μιας 1-1 συνάρτησης f :A → ℝ; Απάντηση Από τον τρόπο που ορίστηκε η g προκύπτει οτι: — έχει πεδίο ορισμού το σύνολο τιμών f (A) της f, — έχει σύνολο τιμών το πεδίο ορισμού Α της f και — ισχύει η ισοδυναμία: f (x) = y ↔ g (y) = x. Αυτό σημαίνει ότι, αν η f αντιστοιχίζει το x στο y, τότε η g αντιστοιχίζει το y στο x και αντιστρόφως. Δηλαδή η g είναι η αντίστροφη διαδικασία της f. Για το λόγο αυτό η g λέγεται αντίστροφη συνάρτηση της f και συμβολίζεται με f-1. Επομένως έχουμε f (x) = y ↔ f-1 (y) = x ,οπότε f-1 (f (x)) = x , x∈A και f (f-1 (y)) = y , y∈f (A).
Έστω μια συνάρτηση f :A → ℝ.Αν υποθέσουμε οτι αυτή είναι 1-1 ,τότε για κάθε στοιχείο y του συνόλου τιμών, f (A) της f , υπάρχει μοναδικό στοιχείο x του πεδίου ορισμού της Α για το οποίο ισχύει f (x) = y . Επομένως ορίζεται μια συνάρτηση g:f (A)→ ℝ με την οποία κάθε y∈f (A) αντιστοιχίζεται στο μοναδικό x∈A για το οποίο ισχύει f (x) = y .
19.Ποιος είναι ο άξονας συμμετρίας των f και f-1; Απάντηση Οι γραφικές παραστάσεις C και C΄των συναρτήσεων f και f-1 είναι συμμετρικές ως προς την ευθεία y = x ,που διχοτομεί τις γωνίες xOy και x΄O y΄. .
20.Να δώσετε τον ορισμού του ορίου μιας συνάρτησης f καθώς το x τείνει στο x0. Απάντηση Όταν οι τιμές μιας συνάρτησης f προσεγγίζουν όσο θέλουμε έναν πραγματικό αριθμό l, καθώς το x προσεγγίζει με οποιονδήποτε τρόπο τον αριθμό x0, τότε γράφουμε ΣΧΟΛΙΟ — Για να αναζητήσουμε το όριο της f στο x0 , πρέπει η f να ορίζεται όσο θέλουμε “κοντά στο x0 ”, δηλαδή η f να είναι ορισμένη σ’ ένα σύνολο της μορφής (α,x0)∪(x0,β) ή (α,x0) ή (x0,β). — Το x0 μπορεί να ανήκει στο πεδίο ορισμού της συνάρτησης ή να μην ανήκει σ’ αυτό . — Η τιμή της f στο x0, όταν υπάρχει, μπορεί να είναι ίση με το όριό της στο x0 ή διαφορετική από αυτό.
= l και διαβάζουμε “το όριο της f (x), όταν το x τείνει στο x0 , είναι l ” ή “το όριο της f (x) στο x0 είναι l ”.
21.Τι ονομάζουμε πλευρικά όρια της f ; Γράψτε τη ιδιότητα των πλευρικών ορίων. Απάντηση Όταν οι τιμές μιας συνάρτησης f προσεγγίζουν όσο θέλουμε τον πραγματικό αριθμό l1, καθώς το x προσεγγίζει το x0 από μικρότερες τιμές (x < x0), τότε γράφουμε: Όταν οι τιμές μιας συνάρτησης f προσεγγίζουν όσο θέλουμε τον πραγματικό αριθμό l2, καθώς το x προσεγγίζει το x0 από μεγαλύτερες τιμές (x > x0), τότε γράφουμε: Τους αριθμούς l1 = Ισχύει οτι:
= l1 και διαβάζουμε: “το όριο της f (x), όταν το x τείνει στο x0 από τα αριστερά, είναι l1”.
= l2 και διαβάζουμε: “το όριο της f (x), όταν το x τείνει στο x0 από τα δεξιά, είναι l2”. και l2 = τους λέμε πλευρικά όρια της f στο x0 και συγκεκριμένα το l1 αριστερό όριο της f στο x0, ενώ το l2 δεξιό όριο της f στο x0. = l αν και μόνο άν = = l.
22.Να γράψετε το όριο της ταυτοτικής και της σταθερής συνάρτησης. Απάντηση
.
.
.
25.Να διατυπώσετε το Κριτήριο παρεμβολής. Απάντηση Έστω οι συναρτήσεις f , g , h . Αν τότε
,
.
26.Να συγκρίνετε τους αριθμούς |ημx| και |x|. Πότε ισχύει η ισότητα; Απάντηση
Για κάθε x∈ℝ ισχύει |ημx|≤|x|. Η ισότητα ισχύει μόνο όταν x = 0.
27.Πότε μπορούμε να αναζητήσουμε τα όρια 
και 
;
Απάντηση
Για να έχει νόημα το όριο πρέπει η f να είναι ορισμένη σε ένα διάστημα της μορφής (α,+∞). Για να έχει νόημα το όριο πρέπει η f να είναι ορισμένη σε ένα διάστημα της μορφής (-∞,β).
28.Τι ονομάζεται ακολουθία; Απάντηση Ακολουθία ονομάζεται κάθε πραγματική συνάρτηση α: ℕ* → ℝ.
29.Πότε μια συνάρτηση f είναι συνεχής σε ένα σημείο x0 του πεδίου ορισμού της; Απάντηση
Έστω μια συνάρτηση f και x0 ένα σημείο του πεδίου ορισμού της. Θα λέμε ότι η f είναι συνεχής στοx0 αν ισχύει οτι = f(x0).
30.Πότε μια συνάρτηση f θα λέμε ότι είναι συνεχής στο ανοικτό διάστημα (α ,β); Απάντηση
Μια συνάρτηση f θα λέμε οτι είναι συνεχής στο (α,β) όταν είναι συνεχής για κάθε x0 ∈(α,β).
31.Πότε μια συνάρτηση f θα λέμε ότι είναι συνεχής στο κλειστό διάστημα [α ,β]; Απάντηση
Μια συνάρτηση f θα λέμε οτι είναι συνεχής στο [α,β] όταν είναι συνεχής για κάθε x0 ∈(α,β) και επιπλέον ισχύει οτι 
= f(α) και 
= f(β) .
32.Να διατυπώσετε το θεώρημα Bolzano. Ποια είναι η γεωμετρική του ερμηνεία; Απάντηση Γεωμετρική ερμηνεία του Θ.Bolzano: Στο παρακάτω σχήμα έχουμε τη γραφική παράσταση μιας συνεχούς συνάρτησης f στο [α,β] . Επειδή τα σημεία A(α ,f (α)) και B(β ,f (β)) βρίσκονται εκατέρωθεν του άξονα x΄x , η γραφική παράσταση της f τέμνει τον x΄x σε ένα τουλάχιστον σημείο. ΣΧΟΛΙΟ Από το θεώρημα του Bolzano προκύπτει ότι: Συγκεκριμένα, ο προσδιορισμός αυτός γίνεται ως εξής: α) Βρίσκουμε τις ρίζες της f. β) Σε καθένα από τα υποδιαστήματα που ορίζουν οι διαδοχικές ρίζες, επιλέγουμε έναν αριθμό και βρίσκουμε το πρόσημο της f στον αριθμό αυτό. Το πρόσημο αυτό είναι και το πρόσημο της f στο αντίστοιχο διάστημα.
Έστω μια συνάρτηση f, ορισμένη σε ένα κλειστό διάστημα [α,β]. Αν η f είναι συνεχής στο [α,β] και επιπλέον, ισχύει f(α)·f(β) < 0 , τότε υπάρχει ένα τουλάχιστον x0∈(α,β) ,τέτοιο ώστε f(x0) = 0. Δηλαδή, υπάρχει μια τουλάχιστον ρίζα της εξίσωσης f (x) = 0 στο ανοικτό διάστημα (α,β).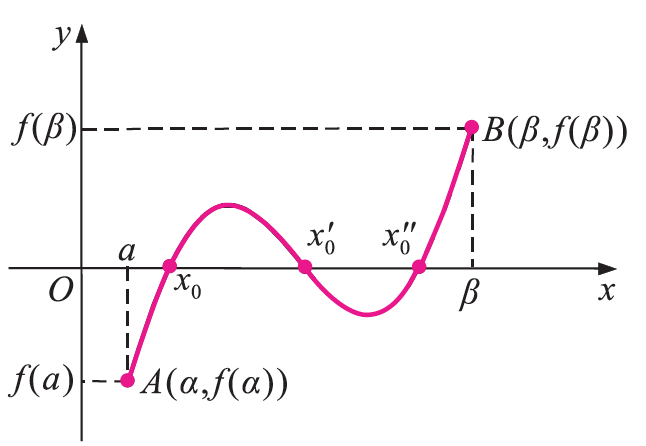
.
33.Διατυπώστε και αποδείξτε το Θεώρημα Ενδιαμέσων Τιμών. Απάντηση Έστω μια συνάρτηση f , η οποία είναι ορισμένη σε ένα κλειστό διάστημα [α,β]. Αν η f είναι συνεχής στο [α,β] και f(α) ≠ f(β), τότε για κάθε αριθμό η μεταξύ των f(α) και f(β) υπάρχει ένας τουλάχιστον αριθμός x0 ∈(α,β) τέτοιος ώστε f(x0) = η. Απόδειξη Έστω ότι f(α) < f(β) και f(α) < η < f(β). Αν θεωρήσουμε τη συνάρτηση g(x) = f(x) – η, x∈[α,β] παρατηρούμε ότι:Η g είναι συνεχής στο [α,β] και g(α)g(β) < 0, αφού g(α) = f(α) – η < 0 και g(β) = f(β) – η > 0. Επομένως, σύμφωνα με το θεώρημα του Bolzano, υπάρχει x0 ∈(α,β) τέτοιο, ώστε g(x0) = f(x0) – η = 0 οπότε f(x0) = η. ΣΧΟΛΙΑ Αν μια συνάρτηση f δεν είναι συνεχής στο διάστημα [α,β] , τότε δεν παίρνει υποχρεωτικά όλες τις ενδιάμεσες τιμές. Με τη βοήθεια του θεωρήματος ενδιαμέσων τιμών αποδεικνύεται ότι: Η εικόνα f (Δ) ενός διαστήματος Δ μέσω μιας συνεχούς και μη σταθερής συνάρτησης f είναι διάστημα.
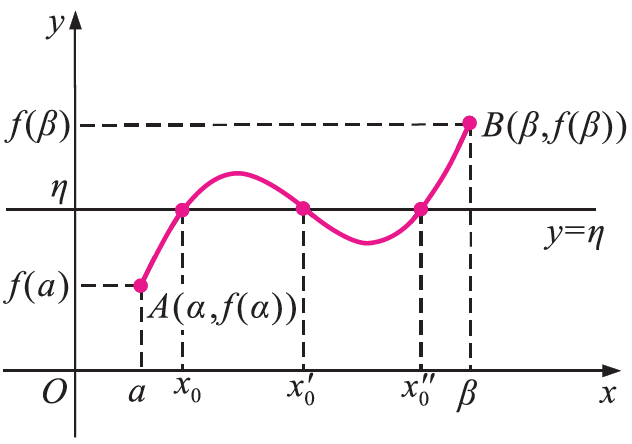
34.Να διατυπώσετε το θεώρημα της μέγιστης και της ελάχιστης τιμής. Απάντηση Δηλαδή, υπάρχουν x1,x2∈[α,β] τέτοια, ώστε, αν m = f(x1) και M = f(x2) , να ισχύει m ≤ f(x) ≤ M,για κάθε x∈[α,β] . ΣΧΟΛΙΟ Από το παραπάνω θεώρημα και το θεώρημα ενδιάμεσων τιμών προκύπτει ότι το σύνολο τιμών μιας συνεχούς συνάρτησης f με πεδίο ορισμού το [α,β] είναι το κλειστό διάστημα [m,M], όπου m η ελάχιστη τιμή και Μ η μέγιστη τιμή της.
Αν f είναι συνεχής συνάρτηση στο [α,β], τότε η f παίρνει στο [α,β] μια μέγιστη τιμή M και μια ελάχιστη τιμή m.
35.Πως συνδέεται η συνέχεια μιας συνάρτησης f με το σύνολο τιμών της; Απάντηση Αν, όμως, η f είναι γνησίως φθίνουσα και συνεχής στο (α,β) , τότε το σύνολο τιμών της στο διάστημα αυτό είναι το διάστημα (B,A) .
Aν μια συνάρτηση f είναι γνησίως αύξουσα και συνεχής σε ένα ανοικτό διάστημα (α,β) τότε το σύνολο τιμών της στο διάστημα αυτό είναι το διάστημα ( Α,Β) ,όπου Α = και Β = .
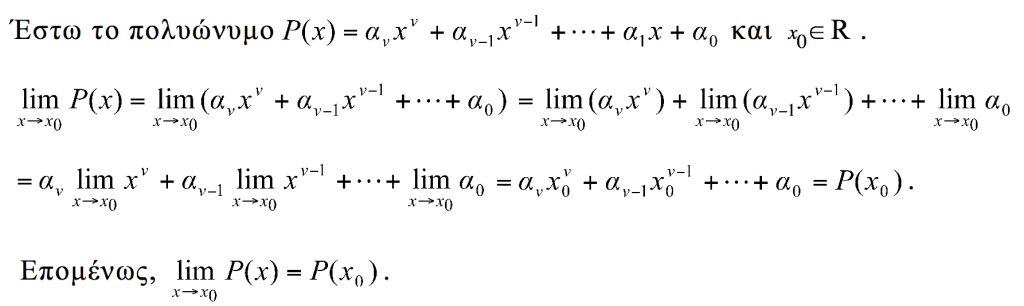
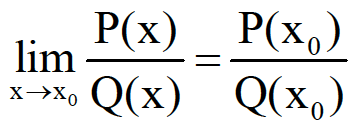