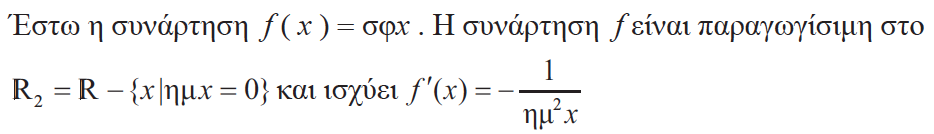16.Να γράψετε την παράγωγο της συνάρτησης f (x) = ex. Απάντηση Η συνάρτηση f (x) = ex ,είναι παραγωγίσιμη στο ℝ με f΄(x) = ex , δηλαδή (ex )΄= ex .
17.Να γράψετε την παράγωγο της συνάρτησης f (x) = lnx. Απάντηση Η συνάρτηση f (x) = lnx ,είναι παραγωγίσιμη στο (0,+∞) με f΄(x) =
, δηλαδή (lnx)΄=
.
18.Να αποδείξετε οτι αν οι συναρτήσεις f , g είναι παραγωγίσιμες στο x0 , τότε η συνάρτηση f +g είναι παραγωγίσιμη στο x0 και ισχύει (f + g)΄(x0) = f΄(x0) + g΄(x0). Απάντηση
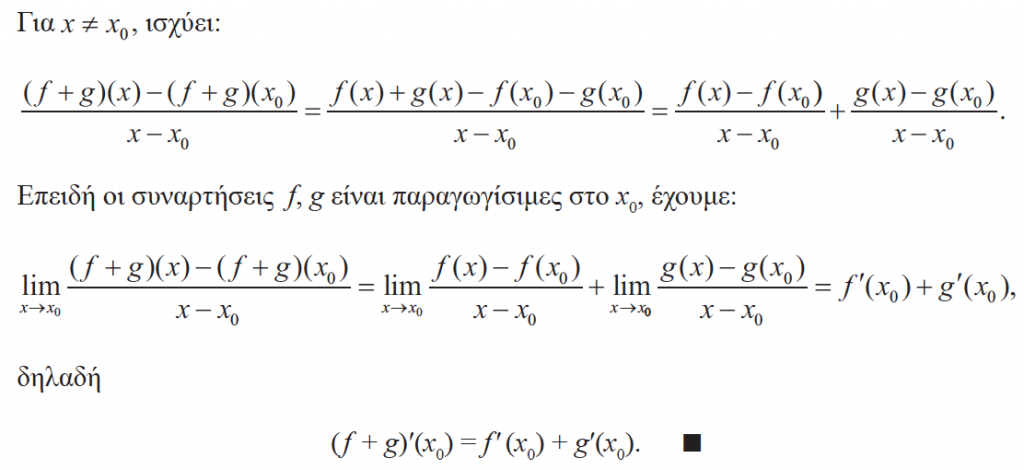
19.Να δείξετε οτι η συνάρτηση f(x) = x-ν ,ν∈ℕ* είναι παραγωγίσιμη στο ℝ* με f΄(x) = -ν·x-ν-1 ,δηλαδή (x-ν)΄= -ν·x-ν-1 . Απάντηση

Απάντηση ,δηλαδή (εφx)΄=
.
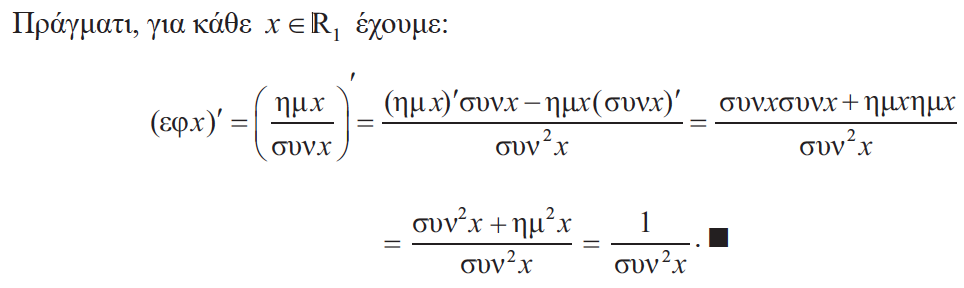
22.Τι γνωρίζετε για τη παράγωγο της fog ; Απάντηση Αν η συνάρτηση g είναι παραγωγίσιμη στο x0 και η f είναι παραγωγίσιμη στο g(x0), τότε η συνάρτηση fog είναι παραγωγίσιμη στο x0 και ισχύει (fog)΄(x0) = f΄(g(x0))·g΄(x0). Γενικά, αν μια συνάρτηση g είναι παραγωγίσιμη σε ένα διάστημα Δ και η f είναι παραγωγίσιμη στο g(Δ) , τότε η συνάρτηση fog είναι παραγωγίσιμη στο Δ και ισχύει (fog)΄(x) = f΄(g(x))·g΄(x) Δηλαδή, αν u = g(x), τότε (f(u))΄= f΄(u)·u΄.
23.Να δείξετε ότι η συνάρτηση f (x) = xα, α ∈ ℝ – ℤ είναι παραγωγίσιμη στο (0,+∞) με f΄(x) = α·xα-1 ,δηλαδή (xα)΄= α·xα-1 . Απάντηση
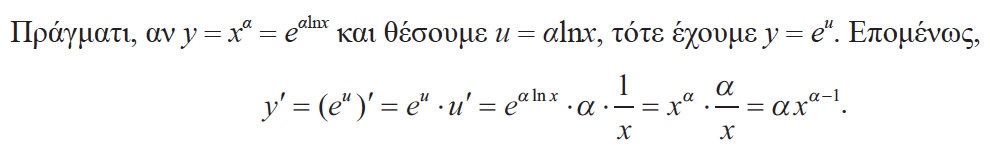
24.Να δείξετε οτι η συνάρτηση f(x) = αx ,α > 0 είναι παραγωγίσιμη στο ℝ με f΄(x) = αx lnα ,δηλαδή (αx)΄= αx lnα . Απάντηση Πράγματι, αν y = αx = exlnα και θέσουμε u = xlnα, τότε έχουμε y = eu. Επομένως, y΄ = (eu)΄=eu ·u΄= exlnα ·lnα = αx·lnα. .
25.Να δείξετε οτι η συνάρτηση f(x) = ln|x| ,x∈ ℝ* είναι παραγωγίσιμη στο ℝ* με f΄(x) = Απάντηση ,δηλαδή (ln|x|)΄=
.
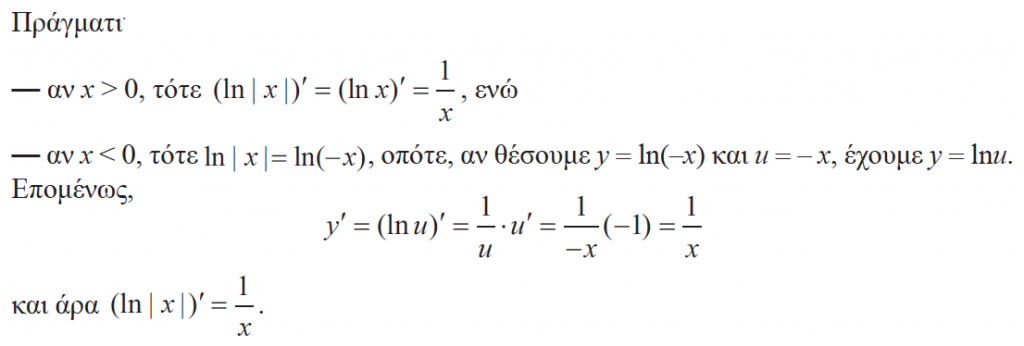
26. Τι ονομάζουμε ρυθμό μεταβολής του y ως προς το x στο σημείο x0; Απάντηση
Αν δύο μεταβλητά μεγέθη x, y συνδέονται με τη σχέση y = f (x) , όταν f είναι μια συνάρτηση παραγωγίσιμη στο x0 , τότε ονομάζουμε ρυθμό μεταβολής του y ως προς το x στο σημείο x0 την παράγωγο f ΄(x0) .
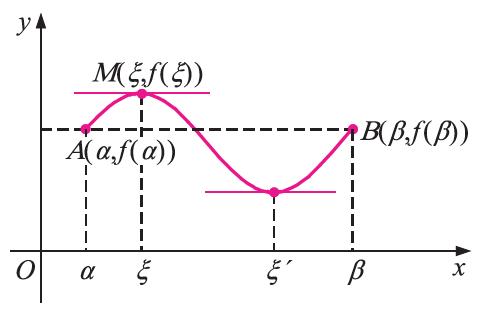
27. Να διατυπώσετε το Θεώρημα Rolle και να αποδώσετε τη γεωμετρική του ερμηνεία. Απάντηση Αν μια συνάρτηση f είναι συνεχής στο κλειστό διάστημα [α, β] , παραγωγίσιμη στο ανοικτό διάστημα (α, β) και f (α) = f (β) ,τότε υπάρχει ένα, τουλάχιστον, ξ ∈(α, β) τέτοιο, ώστε: f ΄(ξ) = 0 . Γεωμετρικά, αυτό σημαίνει ότι υπάρχει ένα, τουλάχιστον, ξ∈(α, β) τέτοιο, ώστε η εφαπτομένη της Cf στο M(ξ, f (ξ)) να είναι παράλληλη στον άξονα των x.
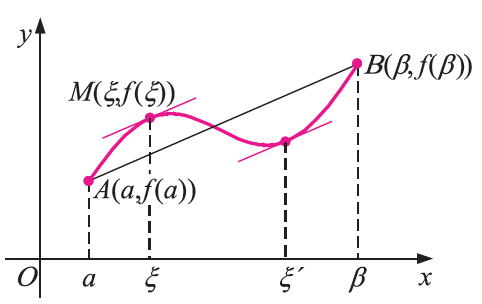
28.Να διατυπώσετε το Θεώρημα Μέσης Τιμής και να αποδώσετε τη γεωμετρική του ερμηνεία. Απάντηση Αν μια συνάρτηση f είναι συνεχής στο κλειστό διάστημα [α, β] και παραγωγίσιμη στο ανοικτό διάστημα (α, β) ,τότε υπάρχει ένα, τουλάχιστον, ξ ∈(α, β) τέτοιο, ώστε: f ΄(ξ) = Γεωμετρικά, αυτό σημαίνει ότι υπάρχει ένα, τουλάχιστον, ξ∈(α, β) τέτοιο, ώστε η εφαπτομένη της Cf στο M(ξ, f (ξ)) να είναι παράλληλη της ευθείας ΑΒ ,όπου Α(α,f(α)) και Β(β,f(β)).
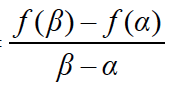 .
.
Απάντηση Αρκεί να αποδείξουμε ότι για οποιαδήποτε x1, x2 ∈Δ ισχύει f(x1) = f(x2). Πράγματι Σε όλες τις περιπτώσεις λοιπόν είναι f(x1) = f(x2).
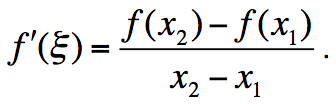 (1)
(1)
Απάντηση
Η συνάρτηση f – g είναι συνεχής στο Δ και για κάθε εσωτερικό σημείο x ∈Δ ισχύει
31.Έστω μια συνάρτηση f, η οποία είναι συνεχής σε ένα διάστημα Δ. Αν f΄(x) > 0 σε κάθε εσωτερικό σημείο x του Δ, τότε να αποδείξετε ότι η f είναι γνησίως αύξουσα σε όλο το Δ. Απάντηση Έστω x1,x2 ∈Δ με x1 < x2. Θα δείξουμε ότι f (x1) < f (x2). Πράγματι, στο διάστημα [x1 , x2] η f ικανοποιεί τις προϋποθέσεις του Θ.Μ.Τ. Επομένως υπάρχει ξ ∈(x1 , x2) τέτοιο, ώστε ΣΧΟΛΙΟ Αναλόγως εργαζόμαστε στην περίπτωση που είναι f΄(x) < 0 και το θεώρημα δίνοταν ως εξής: Έστω μια συνάρτηση f, η οποία είναι συνεχής σε ένα διάστημα Δ. Αν f΄(x) < 0 σε κάθε εσωτερικό σημείο x του Δ, τότε να αποδείξετε ότι η f είναι γνησίως φθίνουσα σε όλο το Δ.
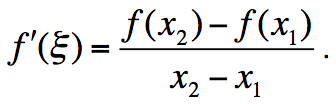 Oπότε έχουμε f (x2) – f (x1) = f΄(ξ)(x2 – x1).
Oπότε έχουμε f (x2) – f (x1) = f΄(ξ)(x2 – x1).
Επειδή f΄(ξ) > 0 και x2 – x1 > 0 έχουμε f (x2) – f (x1) > 0 οπότε f (x1) <f (x2).
32.Πότε μια συνάρτηση f ,με πεδίο ορισμού το Α, θα λέμε ότι παρουσιάζει στο x0∈Α τοπικό μέγιστο; Απάντηση Μια συνάρτηση f, με πεδίο ορισμού Α, θα λέμε ότι παρουσιάζει στο x0 ∈Α τοπικό μέγιστο, όταν υπάρχει δ > 0 , τέτοιο ώστε f (x) ≤ f (x0) για κάθε x∈A∩(x0-δ , x0+δ) .To x0 λέγεται θέση ή σημείο τοπικού μεγίστου, ενώ το f (x0) τοπικό μέγιστο της f.