1.Ποιο πείραμα ονομάζεται αιτιοκρατικό;

Απάντηση
Κάθε πείραμα κατά το οποίο η γνώση των συνθηκών κάτω από τις οποίες εκτελείται καθορίζει πλήρως το αποτέλεσμα λέγεται αιτιοκρατικό (deterministic) πείραμα. 

2.Τι ονομάζουμε πείραμα τύχης; 

Απάντηση
Πείραμα τύχης (random experiment) ονομάζεται το πείραμα του οποίου δεν μπορούμε εκ των προτέρων να προβλέψουμε το αποτέλεσμα, μολονότι επαναλαμβάνεται (φαινομενικά τουλάχιστον) κάτω από τις ίδιες συνθήκες.  

3.Τι λέγεται δειγματικός χώρος ενός πειράματος τύχης; 

Απάντηση

Όλα τα αποτελέσματα που μπορούν να εμφανιστούν σε ένα πείραμα τύχης λέγονται δυνατά αποτελέσματα ή δυνατές περιπτώσεις του πειράματος. Το σύνολο των δυνατών αποτελεσμάτων λέγεται δειγματικός χώρος (sample space) και συμβολίζεται συνήθως με το γράμμα Ω. Αν δηλαδή ω₁, ω₂, …, ω_κ είναι τα δυνατά αποτελέσματα ενός πειράματος τύχης, τότε ο δειγματικός χώρος του πειράματος θα είναι το σύνολο: Ω ={ ω₁, ω₂, …, ω_κ }.

4.Τι ονομάζεται ενδεχόμενο ή γεγονός;

Απάντηση

Το σύνολο που έχει ως στοιχεία ένα ή περισσότερα αποτελέσματα ενός πειράματος τύχης λέγεται ενδεχόμενο (event) ή γεγονός. 

5.Τι λέγεται απλό και τι σύνθετο ενδεχόμενο ενός πείραμα τύχης; 

Απάντηση

Ένα ενδεχόμενο λέγεται απλό όταν έχει ένα μόνο στοιχείο και σύνθετο αν έχει περισσότερα στοιχεία.  

6.Ποτε λέμε ότι ένα ενδεχόμενο Α ενός πειράματος τύχης  πραγματοποιείται ή συμβαίνει σε μια συγκεκριμένη εκτέλεσή του πειράματος; 

Απάντηση
Όταν το αποτέλεσμα ενός πειράματος, σε αυτή την εκτέλεσή είναι στοιχείο του ενδεχομένου Α. 

Απάντηση

Ευνοϊκές περιπτώσεις για την πραγματοποίησή ενός ενδεχομένου ονομάζουμε τα στοιχεία του ενδεχομένου. 

8.Τι ονομάζουμε βέβαιο και τι αδύνατο ενδεχόμενο;

Απάντηση
Ο ίδιος ο δειγματικός χώρος Ω ενός πειράματος θεωρείται ότι είναι ενδεχόμενο, το οποίο μάλιστα πραγματοποιείται πάντοτε, αφού όποιο και αν είναι το αποτέλεσμα του πειράματος θα ανήκει στο Ω. Γι’ αυτό το Ω λέγεται βέβαιο ενδεχόμενο. Δεχόμαστε ακόμα ως ενδεχόμενο και το κενό σύνολο Ø που δεν πραγματοποιείται σε καμιά εκτέλεση του πειράματος τύχης. Γι’ αυτό λέμε ότι το Ø είναι το αδύνατο ενδεχόμενο.  

9.Αν Α είναι ένα ενδεχόμενο τι συμβολίζει το N(A) ;

Απάντηση
Συμβολίζουμε το πλήθος των στοιχείων του ενδεχομένου Α.  

10.Πότε πραγματοποιείται το ενδεχόμενο ; Να παραστήσετε το  σε ένα διάγραμμα του Venn. 

Απάντηση
Το ενδεχόμενο  , διαβάζεται  “Α τομή Β”  ή “Α και Β”  “Α τομή Β” ή “Α και Β”  πραγματοποιείται, όταν πραγματοποιούνται συγχρόνως τα  Α και  Β.

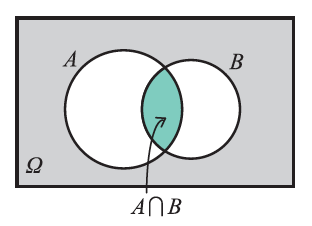
11.Πότε πραγματοποιείται το ενδεχόμενο ; Να παραστήσετε το  σε ένα διάγραμμα του Venn.

Απάντηση
Tο ενδεχόμενο ,  διαβάζεται “Α ένωση Β” ή “Α ή Β” , πραγματοποιείται, όταν πραγματοποιείται ένα τουλάχιστον από τα  Α,  Β. 

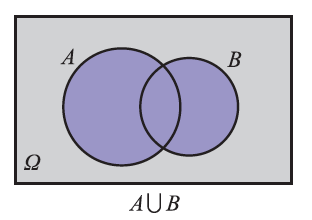
12.Πότε πραγματοποιείται το αντίθετο ενδεχόμενο  A′ του A ; Να παραστήσετε το A′ σε ένα διάγραμμα του Venn ;

Απάντηση
Tο ενδεχόμενο A΄ , διαβάζεται “όχι το Α” ή “συμπληρωματικό του Α”  πραγματοποιείται, όταν δεν πραγματοποιείται το Α. Το A΄ λέγεται και “αντίθετο του Α”. 

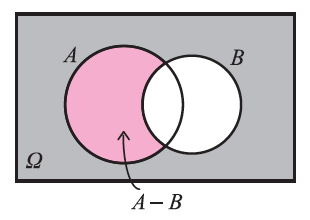
13.Πότε πραγματοποιείται η διαφορά A – B του B από το A ; Να παραστήσετε το A – B σε ένα διάγραμμα του Venn.

Απάντηση
Tο ενδεχόμενο A – B, διαβάζεται “διαφορά του Β από το Α”  πραγματοποιείται, όταν πραγματοποιείται το Α αλλά όχι το Β. Είναι εύκολο να δούμε ότι  .

ΣΧΟΛΙΟ

Στον παρακάτω πίνακα τα Α και Β συμβολίζουν ενδεχόμενα ενός πειράματος και το ω ένα αποτέλεσμα του πειράματος αυτού. Στην αριστερή στήλη του πίνακα αναγράφονται διάφορες σχέσεις για τα Α και Β διατυπωμένες στην κοινή γλώσσα, και στη δεξιά στήλη αναγράφονται οι ίδιες σχέσεις αλλά διατυπωμένες στη γλώσσα των συνόλων.

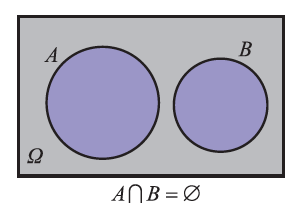
14.Πότε δύο ενδεχόμενα λέγονται ασυμβίβαστα  ή ξένα μεταξύ τους ή αμοιβαίως αποκλειόμενα.

Απάντηση

Δύο ενδεχόμενα Α και Β λέγονται ασυμβίβαστα, όταν  .

Απάντηση

Οι σχετικές συχνότητες πραγματοποίησης των ενδεχομένων ενός πειράματος σταθεροποιούνται γύρω από κάποιους αριθμούς (όχι πάντοτε ίδιους), καθώς ο αριθμός των δοκιμών του πειράματος επαναλαμβάνεται απεριόριστα. Το εμπειρικό αυτό εξαγόμενο, το οποίο επιβεβαιώνεται και θεωρητικά, ονομάζεται στατιστική ομαλότητα ή νόμος των μεγάλων αριθμών.

Απάντηση

Σε ένα πείραμα με ισοπίθανα αποτελέσματα  ορίζουμε ως πιθανότητα του ενδεχομένου Α τον αριθμό:

.

ΣΧΟΛΙΟ

Από τον προηγούμενο ορισμό προκύπτει άμεσα ότι: 

 Για κάθε ενδεχόμενο Α ισχύει  , αφού το πλήθος των στοιχείων ενός ενδεχομένου είναι ίσο ή μικρότερο από το πλήθος των στοιχείων του δειγματικού χώρου.

Απάντηση

Έστω Ω ={ ω₁, ω₂, …, ω_v } ένας δειγματικός χώρος με πεπερασμένο πλήθος στοιχείων. Σε κάθε απλό ενδεχόμενο {ω_i} αντιστοιχίζουμε έναν πραγματικό αριθμό, που τον συμβολίζουμε με P (ω_i) , έτσι ώστε να ισχύουν:

Τον αριθμό P (ω_i) ονομάζουμε πιθανότητα του ενδεχομένου {ω_i}. Ως πιθανότητα Ρ(Α) ενός ενδεχομένου A = {α₁ , α₂ ,…, α_κ} ≠ ∅ ορίζουμε το άθροισμα Ρ(α₁) + Ρ(α₂) +…+ Ρ(α_κ) , ενώ ως πιθανότητα του αδύνατου ενδεχομένου  ∅ ορίζουμε τον αριθμό P(∅) = 0.

18.Να αποδείξετε ότι για οποιαδήποτε ασυμβίβαστα μεταξύ τους ενδεχόμενα  Α και  Β ισχύει ο απλός προσθετικός νόμος:  .

Απάντηση

Αν N(A) = κ και N(B) = λ , τότε το έχει κ + λ στοιχεία, γιατί αλλιώς τα Α και Β δε θα ήταν ασυμβίβαστα. Δηλαδή, έχουμε = κ + λ =.
Επομένως:
 .

19.Να αποδείξετε ότι για δύο συμπληρωματικά ενδεχόμενα  Α  και A′ ισχύει: P(A′) = 1− P(A) .

Απάντηση

Επειδή (A ∩ A′) = ∅ , δηλαδή τα Α και A′ είναι ασυμβίβαστα, έχουμε διαδοχικά, σύμφωνα με τον απλό προσθετικό νόμο:  ,

 ,

,

.

20.Να αποδείξετε ότι για δύο ενδεχόμενα  Α  και  Β  ενός δειγματικού χώρου Ω ισχύει ο προσθετικός νόμος:   .

Απάντηση

Για τα ενδεχόμενα Α και Β ισχύει:

  (1)  αφού στο άθροισμα  N(A)+N(B) το πλήθος

των στοιχείων του ενδεχομένου  υπολογίζεται δύο

φορές. Είναι   , οπότε από την (1) έχουμε:

και επομένως:

.

Η ιδιότητα αυτή είναι γνωστή ως προσθετικός νόμος (additive law).

Απάντηση

Επειδή  έχουμε διαδοχικά: 

 .

22.Να αποδείξετε ότι για δύο ενδεχόμενα Α και Β ενός δειγματικού χώρου Ω ισχύει:  .

Απάντηση

Επειδή τα ενδεχόμενα  και  είναι ασυμβίβαστα και

 , έχουμε:  .

‘Aρα   .