Διανύσματα
Απάντηση Το διάνυσμα ορίζεται ως ένα προσανατολισμένο ευθύγραμμο τμήμα, δηλαδή ως ένα ευθύγραμμο τμήμα του οποίου τα άκρα θεωρούνται διατεταγμένα. Το πρώτο άκρο λέγεται αρχή ή σημείο εφαρμογής του διανύσματος, ενώ το δεύτερο λέγεται πέρας του διανύσματος. Το διάνυσμα με αρχή το Α και πέρας το Β συμβολίζεται με
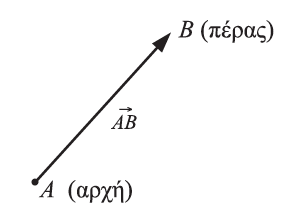
και παριστάνεται με ένα βέλος που ξεκινάει από το Α και καταλήγει στο Β.
Απάντηση Αν η αρχή και το πέρας ενός διανύσματος συμπίπτουν, τότε το διάνυσμα λέγεται μηδενικό διάνυσμα. Έτσι, για παράδειγμα, το διάνυσμα
είναι μηδενικό διάνυσμα.
Απάντηση Η απόσταση των άκρων ενός διανύσματος Αν το διάνυσμα και πότε το
θα λέγεται μοναδιαίο;
, δηλαδή το μήκος του ευθύγραμμου τμήματος ΑΒ, λέγεται μέτρο ή μήκος του διανύσματος
και συμβολίζεται με
.
έχει μέτρο ίσο με 1 , τότε λέγεται μοναδιαίο διάνυσμα.
Απάντηση Η ευθεία πάνω στην οποία βρίσκεται ένα μη μηδενικό διάνυσμα Ως φορέα ενός μηδενικού διανύσματος ΣΧΟΛΙΟ Αν ο φορέας ενός διανύσματος ;

λέγεται φορέας του
.
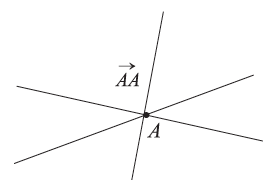
μπορούμε να θεωρούμε οποιαδήποτε από τις ευθείες που διέρχονται από το Α.
είναι παράλληλος ή συμπίπτει με μια ευθεία ζ, τότε λέμε ότι το
είναι παράλληλο προς τη ζ και γράφουμε
//ζ .
Απάντηση Δύο μη μηδενικά διανύσματα Στην περίπτωση αυτή λέμε ότι τα Τα συγγραμμικά διανύσματα διακρίνονται σε ομόρροπα και αντίρροπα. και
λέγονται παράλληλα;

και
, που έχουν τον ίδιο φορέα ή παράλληλους φορείς, λέγονται παράλληλα ή συγγραμμικά διανύσματα.
και
έχουν ίδια διεύθυνση και γράφουμε
.
Απάντηση Δύο μη μηδενικά διανύσματα α) όταν έχουν παράλληλους φορείς και βρίσκονται στο ίδιο ημιεπίπεδο ως προς την ευθεία ΑΓ που ενώνει τις αρχές τους, ή β) όταν έχουν τον ίδιο φορέα και μία από τις ημιευθείες ΑΒ και ΓΔ περιέχει την άλλη. Στις περιπτώσεις αυτές λέμε ότι τα και
λέγονται ομόρροπα;

και
λέγονται ομόρροπα:
και
έχουν την ίδια κατεύθυνση (ίδια διεύθυνση και ίδια φορά) και γράφουμε
.
Απάντηση Δύο μη μηδενικά διανύσματα Στηνπερίπτωση αυτή λέμε ότι τα διανύσματα και
λέγονται αντίρροπα;
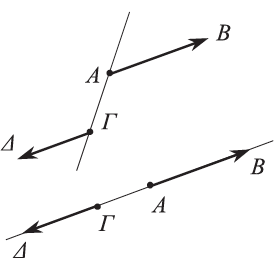
και
λέγονται αντίρροπα , όταν είναι συγγραμμικά και δεν είναι ομόρροπα.
και
έχουν αντίθετη κατεύθυνση (ίδια διεύθυνση και αντίθετη φορά) και γράφουμε
.
Απάντηση Δύο μη μηδενικά διανύσματα λέγονται ίσα όταν έχουν την ίδια κατεύθυνση και ίσα μέτρα. Για να δηλώσουμε ότι δύο διανύσματα Τα μηδενικά διανύσματα θεωρούνται ίσα μεταξύ τους και συμβολίζονται με ΣΧΟΛΙΑ Εύκολα αποδεικνύεται ότι: →Αν →Αν Μ είναι το μέσον του ΑΒ, τότε

και
είναι ίσα ,γράφουμε
.
.
τότε
και
.
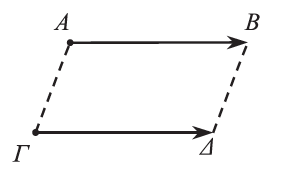
και αντιστρόφως.
![]()
9.Πότε δυο μη μηδενικά διανύσματα λέγονται αντίθετα ; Απάντηση Δύο διανύσματα λέγονται αντίθετα, όταν έχουν αντίθετη κατεύθυνση και ίσα μέτρα. Για να δηλώσουμε ότι δύο διανύσματα ΣΧΟΛΙΟ Είναι φανερό ότι Ειδικότερα, έχουμε

και
είναι αντίθετα, γράφουμε
ή
.
.
.
Απάντηση Έστω δύο μη μηδενικά διανύσματα Την κυρτή γωνία ΣΧΟΛΙΟ Εύκολα αποδεικνύεται ότι η γωνία των →θ = 0 , αν →θ = π , αν →Αν θ = Aν ένα από τα διανύσματα Έτσι, μπορούμε να θεωρήσουμε ότι το μηδενικό διάνυσμα και
;
και
. Με αρχή ένα σημείο Ο παίρνουμε τα διανύσματα
και
.
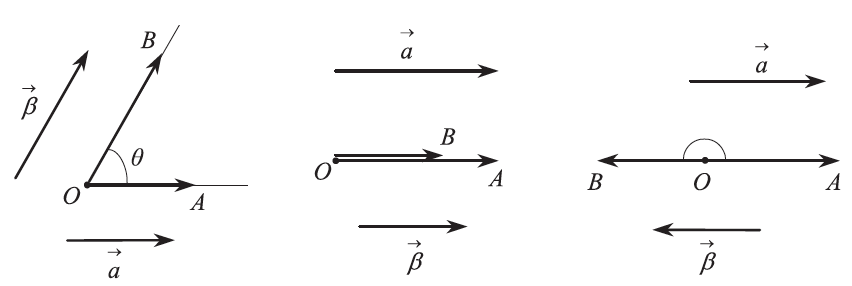
, που ορίζουν οι ημιευθείες ΟΑ και ΟΒ, την ονομάζουμε γωνία των διανυσμάτων
και
και τη συμβολίζουμε με
ή
ή ακόμα, αν δεν προκαλείται σύγχυση, με ένα μικρό γράμμα, για παράδειγμα θ.
και
είναι ανεξάρτητη από την επιλογή του σημείου Ο. Είναι φανερό επίσης ότι 0ο ≤ θ ≤ 180ο ή σε ακτίνια 0 ≤ θ ≤ π και ειδικότερα:
.
.
, τότε λέμε ότι τα διανύσματα
και
είναι ορθογώνια ή κάθετα και γράφουμε
⊥
.
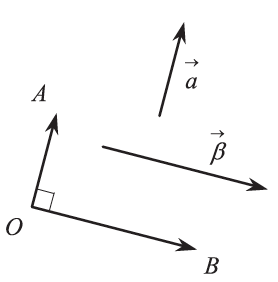
,
είναι το μηδενικό διάνυσμα, τότε ως γωνία των
και
μπορούμε να θεωρήσουμε οποιαδήποτε γωνία θ με 0 ≤ θ ≤ π.
,είναι ομόρροπο ή αντίρροπο ή ακόμη και κάθετο σε κάθε άλλο διάνυσμα.
Απάντηση Έστω δύο διανύσματα.Με αρχή ένα σημείο Ο παίρνουμε διάνυσμα To διάνυσμα Θα αποδείξουμε ότι το άθροισμα των διανυσμάτων Πράγματι, αν O′ είναι ένα άλλο σημείο και πάρουμε τα διανύσματα Επομένως Το άθροισμα δύο διανυσμάτων βρίσκεται και με το λεγόμενο κανόνα του παραλληλόγραμμου. Δηλαδή, αν με αρχή ένα σημείο Ο πάρουμε τα διανύσματα και
.
και στη συνέχεια με αρχή το Α παίρνουμε διάνυσμα
.
λέγεται άθροισμα ή συνισταμένη των διανυσμάτων
και
και συμβολίζεται με
.
και
είναι ανεξάρτητο της επιλογής του σημείου Ο.
και
,επειδή
και
έχουμε
και
.
, που συνεπάγεται ότι και
.
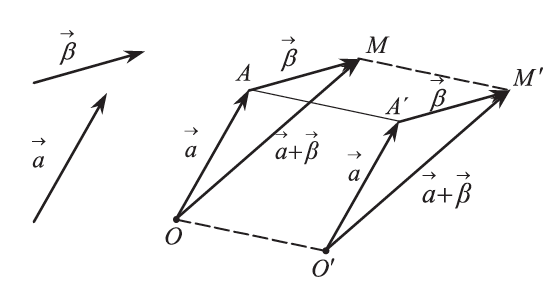
και
, τότε το άθροισμα
ορίζεται από τη διαγώνιο ΟΜ του παραλληλόγραμμου που έχει προσκείμενες πλευρές τις ΟΑ και ΟΒ.
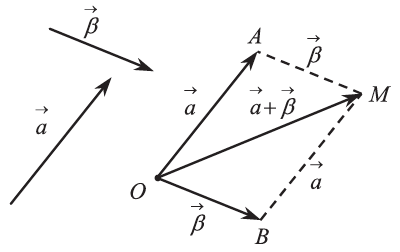
12.Να γράψετε και να αποδείξετε τις ιδιότητες της πρόσθεσης διανυσμάτων. Απάντηση Για την πρόσθεση των διανυσμάτων ισχύουν οι γνωστές ιδιότητες της πρόσθεσης πραγματικών αριθμών. Δηλαδή, αν ΑΠΟΔΕΙΞΕΙΣ (1) Από το παραπάνω σχήμα έχουμε: Επομένως (2) Από το παραπάνω σχήμα έχουμε: και Επομένως, ΣΧΟΛΙΑ Η προσεταιριστική ιδιότητα μας επιτρέπει να συμβολίζουμε καθένα από τα ίσα αθροίσματα Το άθροισμα περισσότερων διανυσμάτων Για παράδειγμα, Δηλαδή, για να προσθέσουμε ν διανύσματα Οι ιδιότητες (3) και (4) είναι προφανείς.
,
,
είναι τρία διανύσματα, τότε:


και
.
.
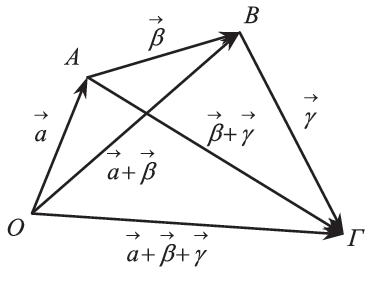
.
.
και
με
,το οποίο θα λέμε άθροισμα των τριών διανυσμάτων
,
και
.
ορίζεται επαγωγικά ως εξής:
.
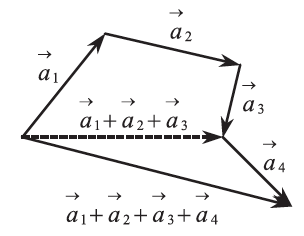
τα καθιστούμε διαδοχικά , οπότε το άθροισμά τους θα είναι το διάνυσμα που έχει ως αρχή την αρχή του πρώτου και ως πέρας το πέρας του τελευταίου. Επειδή μάλιστα ισχύουν η αντιμεταθετική και η προσεταιριστική ιδιότητα της πρόσθεσης, το άθροισμα δε μεταβάλλεται αν αλλάξει η σειρά των προσθετέων ή αν μερικοί από αυτούς αντικατασταθούν με το άθροισμά τους.
Απάντηση Η διαφορά Δηλαδή Σύμφωνα με τα παραπάνω, αν έχουμε δύο διανύσματα Πράγματι, και
.
του διανύσματος
από το διάνυσμα
ορίζεται ως άθροισμα των διανυσμάτων
και
.
.
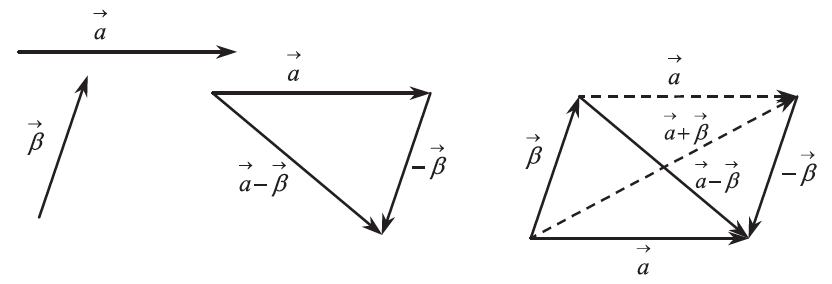
και
τότε υπάρχει μοναδικό διάνυσμα
, τέτοιο, ώστε
.
