Σχολικό βιβλίο (εμπλουτισμένο)
Στην Β΄Γυμνασίου μάθαμε πώς ορίζονται οι τριγωνομετρικοί αριθμοί μιας οξείας γωνίας ορθογωνίου τριγώνου, του οποίου γνωρίζουμε τις πλευρές του. Συγκεκριμένα, μάθαμε ότι:

Φέτος στη Γ΄Γυμνασίου θα ορίσουμε τους τριγωνομετρικούς αριθμούς μιας γωνίας ω με 0°≤ ω ≤ 180° με τη βοήθεια ενός ορθοκανονικού συστήματος αξόνων.
Τοποθετούμε σε ένα ορθοκανονικό σύστημα αξόνων Οxy τη γωνία ω ,έτσι ώστε η κορυφή της να συμπέσει με την αρχή των αξόνων Ο ,η μία πλευρά της να συμπέσει με τον θετικό ημιάξονα Οx και η άλλη της πλευρά να βρεθεί στο 1ο (οξεία) ή 2ο τεταρτημόριο (αμβλεία).
Αν στην πλευρά αυτή πάρουμε ένα οποιοδήποτε σημείο Μ(x, y), διαφορετικό από το Ο, τότε για την απόσταση ρ = ΟΜ ισχύει
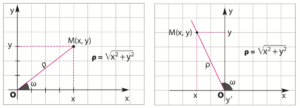
Oι τριγωνομετρικοί αριθμοί της γωνίας ω είναι:

Παρατηρούμε ότι:
- Αν η γωνία ω είναι οξεία, τότε είναι x>0, y>0, ρ>0, οπότε: ημω>0, συνω>0, εφω>0. (1ο τεταρτημόριο)
- Αν η γωνία ω είναι αμβλεία, τότε είναι x<0, y>0, ρ>0, οπότε: ημω>0, συνω<0, εφω<0. (2ο τεταρτημόριο)
- To ημίτονο και το συνημίτονο μιας οποιασδήποτε γωνίας είναι αριθμοί απο -1 έως 1… πχ η ισότητα ημω = -2 είναι αδύνατο να συμβεί!!
Oι προηγούμενοι τύποι γενικεύονται και όταν ω = 0º ή ω = 90º ή ω = 180º.
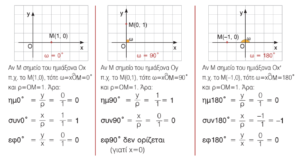
συνοψίζοντας…

Ασκησιολόγιο για την παράγραφο αυτή θα βρείτε στη σελίδα 2

