14.Τι ονομάζουμε διάνυσμα θέσεως ή διανυσματική ακτίνα; Απάντηση Έστω Ο ένα σταθερό σημείο του χώρου. Τότε για κάθε σημείο Μ του χώρου ορίζεται το διάνυσμα Το σημείο Ο, που είναι η κοινή αρχή όλων των διανυσματικών ακτίνων των σημείων του χώρου, λέγεται σημείο αναφοράς στο χώρο. Αν Ο είναι ένα σημείο αναφοράς, τότε για οποιοδήποτε διάνυσμα Δηλαδή:

, το οποίο λέγεται διάνυσμα θέσεως του Μ ή διανυσματική ακτίνα του Μ.
έχουμε
και επομένως
.
“Κάθε διάνυσμα στο χώρο είναι ίσο με τη διανυσματική ακτίνα του πέρατος μείον τη διανυσματική ακτίνα της αρχής”.
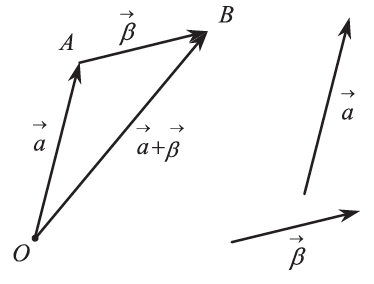
15.Tι γνωρίζεται για το μέτρο αθροίσματος διανυσμάτων; Απάντηση Στο παρακάτω σχήμα βλέπουμε το άθροισμα των διανυσμάτων Από την τριγωνική ανισότητα γνωρίζουμε όμως ότι: |(ΟΑ) – (ΑΒ)|≤ (ΟΒ) ≤ (ΟΑ )+ (ΑΒ) και επομένως
και
.
.
Απάντηση Έστω λ ένας πραγματικός αριθμός με λ ≠ 0 και Είναι ομόρροπο του και έχει μέτρο Αν είναι λ = 0 ή To γινόμενο ;
ένα μη μηδενικό διάνυσμα. Ονομάζουμε γινόμενο του λ με το
και το συμβολίζουμε με
ή
ένα διάνυσμα το οποίο:
, αν λ > 0 και αντίρροπο του
, αν λ < 0
.
, τότε ορίζουμε ως
το μηδενικό διάνυσμα
.
το συμβολίζουμε και με
.
Απάντηση Για το γινόμενο πραγματικού αριθμού με διάνυσμα ισχύουν οι επόμενες ιδιότητες: Ως συνέπεια του ορισμού του γινομένου αριθμού με διάνυσμα και των παραπάνω ιδιοτήτων έχουμε:
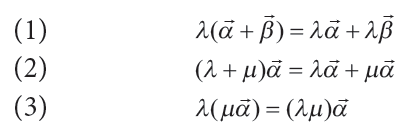
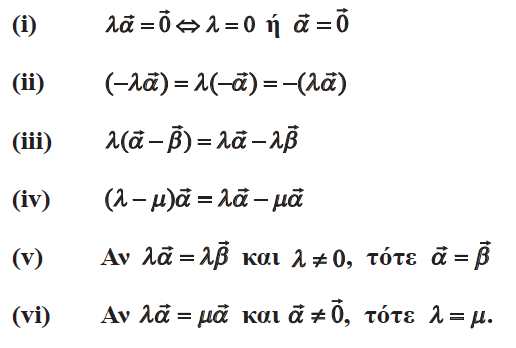
Απάντηση Γραμμικός συνδυασμός δύο διανυσμάτων και
;
και
ονομάζεται κάθε διάνυσμα της μορφής
, όπου κ,λ∈ℝ.
Ανάλογα ορίζεται και ο γραμμικός συνδυασμός τριών ή περισσότερων διανυσμάτων.
Απάντηση Αν δύο διανύσματα Ισχύει όμως και το αντίστροφο. Δηλαδή , αν τα διανύσματα Πράγματι ,αν θέσουμε Συνεπώς: Σε κάθε λοιπόν περίπτωση υπάρχει λ και μάλιστα μοναδικός, τέτοιος, ώστε και
είναι δύο διανύσματα, με
,τότε
(Συνθήκη Παραλληλίας Διανυσμάτων).
και
, όπου
, συνδέονται με τη σχέση
τότε τα διανύσματα αυτά είναι παράλληλα.
και
είναι παράλληλα και
,τότε υπάρχει μοναδικός αριθμός λ τέτοιος ώστε
.
τότε
.
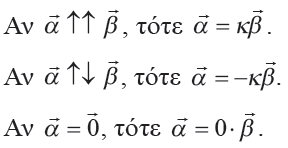
.
Απάντηση Ας πάρουμε ένα διάνυσμα Επειδή ένα διάνυσμα του επιπέδου και Μ το μέσο του ΑΒ τμήματος, να αποδείξετε ότι
.
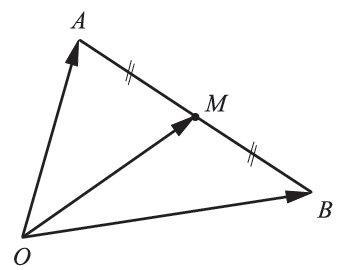
και ένα σημείο αναφοράς Ο.
εχουμε:
,οπότε
και άρα
.
Απάντηση Έστω Οxy ένα σύστημα συντεταγμένων στο επίπεδο και Aν Α1και Α2 οι προβολές του Α στους άξονες x′x και y′y αντιστοίχως, έχουμε: Επομένως x = x΄, που συνεπάγεται ότι και y ≠ y΄. Ώστε: Κάθε διάνυσμα ΣΧΟΛΙΑ Πιο συγκεκριμένα, ο x λέγεται τετμημένη του Από τον τρόπο που ορίστηκαν οι συντεταγμένες ενός διανύσματος προκύπτει ότι: “Δύο διανύσματα είναι ίσα αν και μόνο αν οι αντίστοιχες συντεταγμένες τους είναι ίσες”. Καθένα από τα ίσα διανύσματα με τετμημένη x και τεταγμένη y, θα το συμβολίζουμε με το διατεταγμένο ζεύγος (x , y). γράφεται με μοναδικό τρόπο στη μορφή
,δηλαδή σαν γραμμικός συνυασμός των
και
,όπου
και
τα μοναδιαία διανύσματα των αξόνων x΄x και y΄y αντίστοιχα.
ένα διάνυσμα του επιπέδου. Με αρχή το Ο σχεδιάζουμε το διάνυσμα
.
(1).
Αν x, y είναι οι συντεταγμένες του A, τότε ισχύει και
.Επομένως η ισότητα (1) γράφεται
.
Αποδείξαμε δηλαδή ότι το είναι γραμμικός συνδυασμός των
και
.
Στην παραπάνω κατασκευή οι αριθμοί x και y είναι μοναδικοί.
Θα αποδείξουμε τώρα ότι και η έκφραση του ως γραμμικού συνδυασμού των
και
είναι μοναδική.
Πράγματι, έστω ότι ισχύει και τότε θα έχουμε:
.
Αν υποθέσουμε ότι x ≠ x΄ , δηλαδή ότι x – x΄≠ 0 , τότε θα ισχύει: .
Η σχέση αυτή, όμως, δηλώνει ότι , που είναι άτοπο, αφού τα
και
δεν είναι συγγραμμικά.
του επιπέδου γράφεται κατά μοναδικό τρόπο στη μορφή
.
Τα διανύσματα και
λέγονται συνιστώσες του διανύσματος
κατά τη διεύθυνση των
και
αντιστοίχως , ενώ οι αριθμοί x, y λέγονται συντεταγμένες του
στο σύστημα Οxy.
και ο y λέγεται τεταγμένη του
.
Απάντηση Αν Επομένως , ή ισοδύναμα , ΣΧΟΛΙΟ Γενικότερα , για το γραμμικό συνδυασμό και
,
να αποδείξετε οτι:
και
.
και
,τότε έχουμε:
και
.
και
και
.
έχουμε:
23.Έστω Α(x1 , y1) και Β(x2 , y2) δυο σημεία του επιπέδου.Nα αποδείξετε οτι αν Μ(x , y) μέσο του τμήματος ΑΒ τότε Απάντηση Επομένως ισχύει και
.
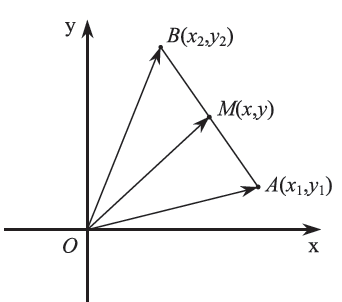
Επειδή και
έχουμε
.
και
.
Απάντηση Ας θεωρήσουμε δύο σημεία Α(x1 , y1) και Β(x2 , y2) του καρτεσιανού επιπέδου και ας υποθέσουμε ότι (x , y) είναι οι συντεταγμένες του διανύσματος Επειδή, έχουμε: ΣΧΟΛΙΟ Συνθήκη Παραλληλίας Διανυσμάτων
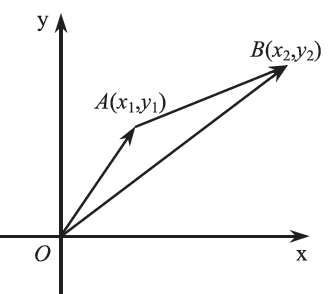
.
.
![]()
Απάντηση Έτσι θα έχουμε: Επομένως το μέτρο του διανύσματος είναι ίσο με
.
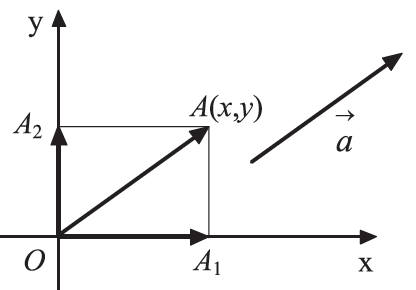
Έστω ένα διάνυσμα του καρτεσιανού επιπέδου και Α το σημείο με διανυσματική ακτίνα
. Αν A1 και A2 είναι οι προβολές του Α στους άξονες x′x και y′y αντιστοίχως, επειδή το σημείο Α έχει τετμημένη x και τεταγμένη y, θα ισχύει (OA1) = |x| και (OA2) = |y| .
.
είναι ίσο με
.
Απάντηση Ας θεωρήσουμε δύο σημεία Α(x1 , y1) και Β(x2 , y2) του καρτεσιανού επιπέδου. Επειδή η απόσταση (AB) των σημείων Α και Β είναι ίση με το μέτρο του διανύσματος Eπομένως η απόσταση των σημείων Α(x1 , y1) και Β(x2 , y2) είναι ίση με .

, σύμφωνα με τον τύπo
θα ισχύει:
.
.
27.Τι ονομάζουμε γωνία που σχηματίζει ένα διάνυσμα Απάντηση Έστω Είναι φανερό ότι 0 ≤ ϕ < 2π . ΣΧΟΛΙΟ Για τη γωνία φ, όπως είναι γνωστό από την Τριγωνομετρία, αν το με τον άξονα x′ x;
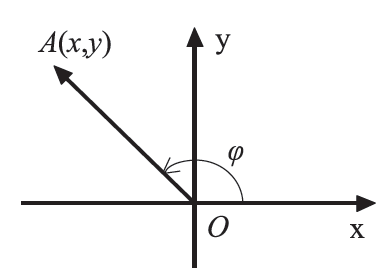
ένα μη μηδενικό διάνυσμα και A το σημείο του επιπέδου για το οποίο ισχύει
. Τη γωνία ϕ , που διαγράφει ο ημιάξονας Οx αν στραφεί γύρω από το Ο κατά τη θετική φορά μέχρι να συμπέσει με την ημιευθεία ΟΑ, την ονομάζουμε γωνία που σχηματίζει το διάνυσμα
με τον άξονα x′ x.
δεν είναι παράλληλο προς τον άξονα y′y, ισχύει
.
