Κωνικές Τομές
Απάντηση Έστω Οxy ένα σύστημα συντεταγμένων στο επίπεδο και C ο κύκλος με κέντρο το σημείο O(0,0) και ακτίνα ρ. Γνωρίζουμε από τη Γεωμετρία ότι ένα σημείο M(x,y) ανήκει στον κύκλο C, αν και μόνο αν απέχει από το κέντρο του Ο απόσταση ίση με ρ, δηλαδή, αν και μόνο αν ισχύει (OM) = ρ. Όμως, Επομένως, η ισότητα (OM) = ρ γράφεται Παρατηρούμε, δηλαδή, ότι οι συντεταγμένες των σημείων του κύκλου και μόνο αυτές επαληθεύουν την εξίσωση Άρα, ο κύκλος με κέντρο το σημείο O(0,0) και ακτίνα ρ έχει εξίσωση ΣΧΟΛΙΟ Ο κύκλος με κέντρο το σημείο O(0,0) και ακτίνα ρ = 1 έχει εξίσωση .
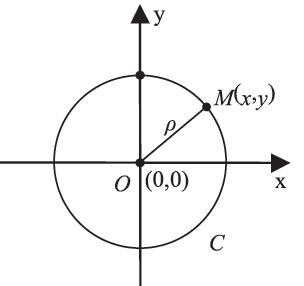
.
ή, ισοδύναμα
.
.
.
και λέγεται μοναδιαίος κύκλος.
Απάντηση Έστω ε η εφαπτομένη του κύκλου C: Γνωρίζουμε από τη Γεωμετρία ότι ένα σημείο M(x , y) ανήκει στην ε, αν και μόνο αν OA⊥AM, δηλαδή, αν και μόνο αν ισχύει Όμως Έτσι η (1) γράφεται διαδοχικά: Επομένως, η εφαπτομένη του κύκλου στο σημείο του Α(x1 , y1) έχει εξίσωση
.
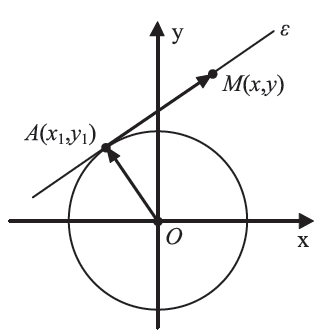
σε ένα σημείο του A(x1 , y1).
. (1)
και
.
αφού
.
στο σημείο του Α(x1 , y1) έχει εξίσωση
.
Απάντηση Έστω Οxy ένα σύστημα συντεταγμένων στο επίπεδο και C ο κύκλος με κέντρο K(x0 , y0) και ακτίνα ρ. Ένα σημείο M(x , y) ανήκει στον κύκλο C, αν και μόνο αν απέχει από το κέντρο του Κ απόσταση ίση με ρ, δηλαδή, αν και μόνο αν ισχύει (KM) = ρ . Όμως, Επομένως, η ισότητα (KM) = ρ γράφεται Άρα, ο κύκλος με κέντρο K(x0 , y0) και ακτίνα ρ έχει εξίσωση .
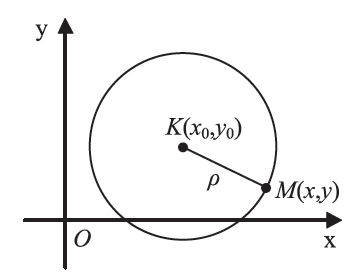
.
ή, ισοδύναμα
.
.
Α2 + Β2 − 4Γ > 0 (1) και αντιστρόφως κάθε εξίσωση της μορφής (1) παριστάνει κύκλο. Απάντηση Έχουμε αποδείξει ότι ο κύκλος με κέντρο K(x0 , y0) και ακτίνα ρ έχει εξίσωση Αν τώρα εκτελέσουμε τις πράξεις, η εξίσωση x2 + y2 − 2x0x − 2y0y + (x02 + y02 − ρ2) = 0 , δηλαδή παίρνει τη μορφή: x2 + y2 + Αx + Βy + Γ = 0 , όπου Α = −2x0 , Β = −2y0 και Γ = x02 + y02 − ρ2 . Αντιστρόφως, κάθε εξίσωση της μορφής x2 + y2 + Αx + Βy + Γ = 0 γράφεται διαδοχικά: Επομένως , αν Α2 + Β2 − 4Γ > 0 η εξίσωση x2 + y2 + Αx + Βy + Γ = 0 παριστάνει κύκλο με κέντρο ΣΧΟΛΙΑ
.
γράφεται:
.
και ακτίνα
.
.
Απάντηση Έστω μια ευθεία δ και ένα σημείο Ε εκτός της δ. Ονομάζεται παραβολή με εστία το σημείο Ε και διευθετούσα την ευθεία δ ο γεωμετρικός τόπος C των σημείων του επιπέδου τα οποία ισαπέχουν από την Ε και τη δ . ΣΧΟΛΙΑ →Αν Α είναι η προβολή της εστίας Ε στη διευθετούσα δ, τότε το μέσο Κ του ΕΑ είναι προφανώς σημείο της παραβολής και λέγεται κορυφή της. →Για να βρούμε ένα σημείο της παραβολής C, εργαζόμαστε ως εξής: Παίρνουμε ένα σημείο Π1 της ημιευθείας ΚΕ και από το σημείο αυτό φέρνουμε την κάθετη στην ΚΕ και έστω Μ1 ένα από τα σημεία τομής της κάθετης αυτής και του κύκλου με κέντρο το Ε και ακτίνα Π1Α. Τότε, το σημείο Μ1 είναι σημείο της παραβολής C. Πράγματι, αν P1 είναι η ορθή προβολή του Μ1 στη διευθετούσα δ, τότε θα ισχύει (Μ1Ρ1) = (Π1Α) = (Μ1Ε) , δηλαδή d(M1 , δ) = d(M1 , E).
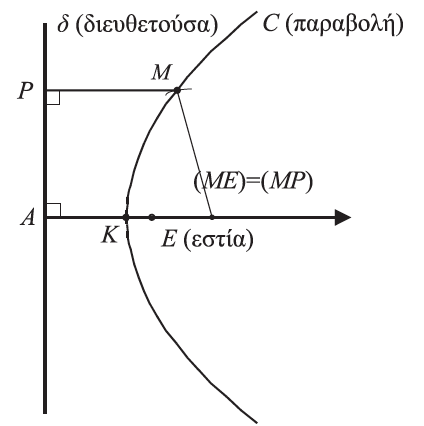
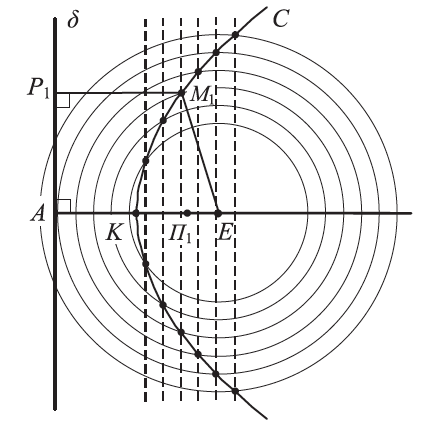
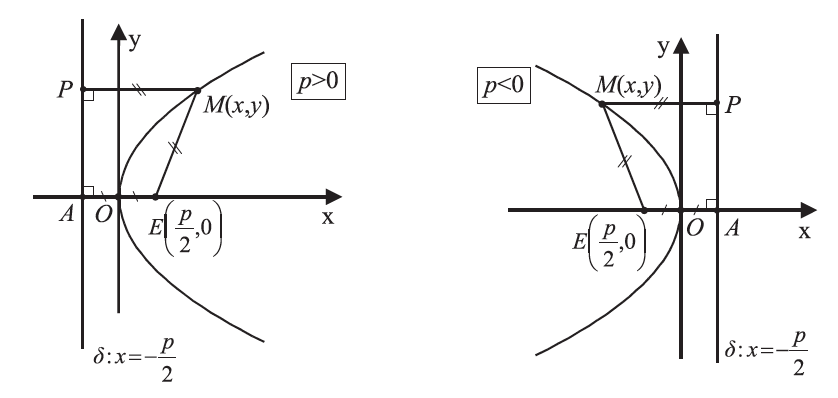
Απάντηση H εξίσωση της παραβολής C με εστία ΣΧΟΛΙΟ Ο αριθμός p λέγεται παράμετρος της παραβολής και η |p| παριστάνει την απόσταση της εστίας από τη διευθετούσα. και διευθετούσα δ:
.
και διευθετούσα δ:
είναι η y2 = 2px .
Απάντηση H εξίσωση της παραβολής C με εστία ΣΧΟΛΙΟ Ο αριθμός p λέγεται παράμετρος της παραβολής και η |p| παριστάνει την απόσταση της εστίας από τη διευθετούσα. και διευθετούσα δ:
.
και διευθετούσα δ:
είναι η x2 = 2py .
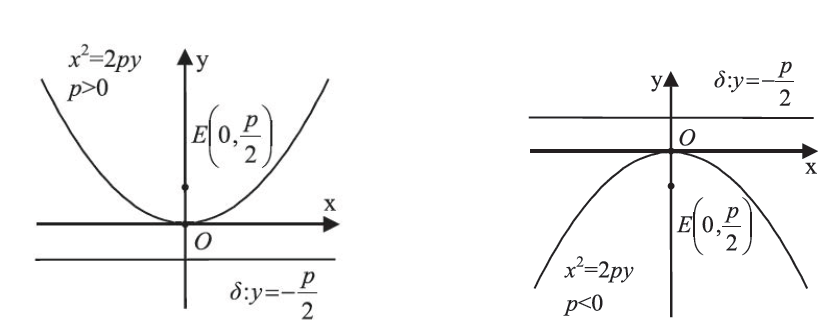
Απάντηση Έστω μια παραβολή y2 = 2px . →Από την εξίσωση y2 = 2px προκύπτει ότι τα p και x (με x ≠ 0 ) είναι ομόσημα. Άρα, κάθε φορά η παραβολή βρίσκεται στο ημιεπίπεδο που ορίζει ο άξονας y′y και η εστία Ε. Επομένως, η παραβολή βρίσκεται στο ημιεπίπεδο που ορίζει η διευθετούσα δ και η εστία Ε. →Aν το σημείο Μ1(x1 , y1) είναι σημείο της παραβολής, δηλαδή, αν y12 = 2px1 ,τότε και το σημείο Μ2(x1 ,−y1) θα είναι σημείο της ίδιας παραβολής, αφού (−y1)2 = 2px1 . Αυτό σημαίνει ότι ο άξονας x′x είναι άξονας συμμετρίας της παραβολής. Επομένως, η κάθετη από την εστία στη διευθετούσα είναι άξονας συμμετρίας της παραβολής και λέγεται άξονας της παραβολής.
Μ1(x1 , y1). Απάντηση H εξίσωση της εφαπτομένης της παραβολής y2 = 2px στο σημείο της Μ1(x1 , y1) είναι yy1 = p(x + x1).
Μ1(x1 , y1). Απάντηση H εξίσωση της εφαπτομένης της παραβολής x2 = 2py στο σημείο της Μ1(x1 , y1) είναι xx1 = p(y + y1).
