Για να ξεκινήσετε πατήστε ΕΚΚΙΝΗΣΗ ΚΟΥΙΖ
Περίληψη κουίζ
Ολοκληρώθηκαν 0 από 10 ερωτήσεις
Ερωτήσεις:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
Πληροφορίες
Διαγώνισμα 1 – Πρόοδοι
Έχεις ήδη ολοκληρώσει το κουίζ. Δεν μπορείς, λοιπόν, να το ξεκινήσεις ξανά.
Το κουίζ φορτώνεται...
Πρέπει να συνδεθείτε ή να εγγραφείτε για να ξεκινήσετε το κουίζ.
Πρέπει να ολοκληρώσεις το επόμενο κουίζ για να ξεκινήσεις αυτό το κουίζ:
Αποτελέσματα
Απαντήθηκαν σωστά 0 από 10 ερωτήσεις
Ο χρόνος σου:
Ό χρόνος πέρασε
Έφτασες 0 από 0 βαθμούς, (0)
Κατηγορίες
- Χωρίς κατηγορία 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- Απαντήθηκε
- Ανασκόπηση
-
Ερώτηση 1 από 10
1. Ερώτηση
2 βαθμοίΑν α, β, γ διαδοχικοί όροι γεωμετρικής προόδου, ισχύει ότι 2β = α + γ.
-
Ερώτηση 2 από 10
2. Ερώτηση
2 βαθμοίΟι όροι 1008, 2016 ,3024 είναι διαδοχικοί όροι αριθμητικής προόδου.
-
Ερώτηση 3 από 10
3. Ερώτηση
2 βαθμοίΟι όροι 1008, 2016 ,4032 είναι διαδοχικοί όροι γεωμετρικής προόδου.
-
Ερώτηση 4 από 10
4. Ερώτηση
2 βαθμοίΑν α, β, γ διαδοχικοί όροι αριθμητικής προόδου, ισχύει ότι 2γ = α + β.
-
Ερώτηση 5 από 10
5. Ερώτηση
2 βαθμοίΑν α, β και γ διαδοχικοί όροι για τους οποίους ισχύει ότι β2 = α · γ , τότε θα είναι διαδοχικοί όροι γεωμετρικής προόδου.
-
Ερώτηση 6 από 10
6. Ερώτηση
2 βαθμοίΣε μια αριθμητική πρόοδο με 1ο όρο τον α1 ισχύει ότι: αν = α1 +(ν-1)ω ,όπου ω η διαφορά της προόδου.
-
Ερώτηση 7 από 10
7. Ερώτηση
2 βαθμοίΣε μια γεωμετρική πρόοδο με 1ο όρο τον α1 ισχύει ότι: αν = α1· λν ,όπου λ ο λόγος της προόδου.
-
Ερώτηση 8 από 10
8. Ερώτηση
2 βαθμοίΙσχύει οτι 2 + 4 + 6 + 8 +…+ 20 = 1 + 3 + 5 + 7 +…+21
-
Ερώτηση 9 από 10
9. Ερώτηση
2 βαθμοίΙσχύει οτι: 2 + 4 + 6 + 8 +…+50 = 650
-
Ερώτηση 10 από 10
10. Ερώτηση
2 βαθμοίΤο άθροισμα των ν πρώτων όρων γεωμετρικής προόδου είναι
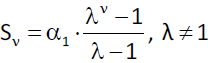
ΚΑΛΗ ΕΠΙΤΥΧΙΑ
